Cho hàm số y = f x có đồ thị như hình vẽ:
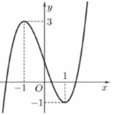
Số nghiệm của phương trình 4 f (x) + 3 = 0 là
A. 3.
B. 0.
C. 1.
D. 2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
2 f x - 1 - 3 = 0 ⇔ f x - 1 = 3 2
Đồ thị hàm số y = f x - 1 có được bằng cách tình tiến đồ thị hàm số y = f(x) sang phải một đơn vị, sau đó lấy đối xứng đồ thị vừa tịnh tiến được qua trục Ox
Ta thấy f x - 1 = 3 2 là sự tương giao giữa đồ thị hàm số y = f x - 1 và đường thẳng y = 3 2 . Dựa vào đồ thị hàm số ta thấy f x - 1 = 3 2 có 4 nghiệm

Đáp án B
Cách 1:
Dựa vào đồ thị suy ra hàm số có dạng bậc 3
Ta có y ' = k x x - 1 ⇒ y = k x 3 2 - x 2 2 + C
Đồ thị qua 2 điểm (0;1),(1;2)
⇒ C = 1 k = - 6 ⇒ y = - 2 x 3 + 3 x 2 + 1 . Từ đó vẽ đồ thị hàm số y = f x - 1
Cách 2:
Từ đồ thị hàm số y = f(x) tịnh tiến sang phải 1 đơn vị ta được đồ thị hàm số y = f(x - 1) từ đó suy ra đồ thị hàm số
y
=
f
x
-
1
như hình bên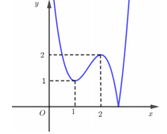
Suy ra phương trình f x - 1 = 3 2 có 4 nghiệm phân biệt

Đáp án B
2 f ( x − 1 ) − 3 = 0 ⇔ f ( x − 1 ) = 3 2
Đồ thị hàm số y = f ( x − 1 ) có được bằng cách tình tiến đồ thị hàm số y = f(x) sang phải một đơn vị, sau đó lấy đối xứng đồ thị vừa tịnh tiến được qua trục Ox
Ta thấy f ( x − 1 ) = 3 2 là sự tương giao giữa đồ thị hàm số y = f ( x − 1 ) và đường thẳng y = 3 2 . Dựa vào đồ thị hàm số ta thấy f ( x − 1 ) = 3 2 có 4 nghiệm

Chọn đáp án D.
Ta có f(x)+3 = 0 → f(x) = -3 dựa vào đồ thị hàm số suy ra phương trình này có 2 nghiệm phân biệt.
Chọn A.
Xét phương trình 4 f x + 3 = 0 ⇔ f x = - 3 4 *
Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số y = f x
và đường thẳng y = - 3 4 (song song với trục hoành)
Từ hình vẽ ta thấy đường thẳng y = - 3 4
cắt đồ thị y = f x tại ba điểm phân biệt nên phương trình đã cho có 3 nghiệm phân biệt