Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a cạnh bên bằng 3a. Tính thể tích V của khối chóp đã cho.
A. V = 4 7 a 3 2
B. V = 4 7 a 3 6
C. V = 7 a 3 3
D. V = 4 7 a 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
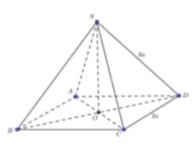
Trong (ABCD). Gọi O=AC ∩ BD Khi đó SO ⊥ (ABCD)
Trong tam giác ABD vuông tại A. Ta có:
B D = A B 2 + A D 2 = 2 a 2 + 2 a 2 = 2 2 a ⇒ B O = 1 2 B D = a 2
Trong tam giác SOB vuông tại O. Ta có:
S O = S B 2 - B O 2 = 3 a 2 + a 2 2 = a 7
V S . A B C D = 1 3 S O . S A B C D = 1 3 . a 7 . 2 a 2 = 4 a 3 7 3

Gọi O là tâm hình vuông ABCD,M là trung điểm của SA
Mặt phẳng trung trực của đoạn thẳng SA cắt SO tại I
Điểm I là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD bán kính R=IS
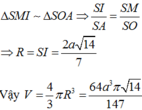
Đáp án C
Đáp án D.