Cho log3 5 = a, log3 6 = b, log3 22 = c. Mệnh đề nào dưới đây đúng?
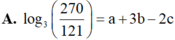
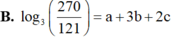
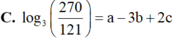
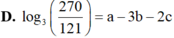
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Phương trình 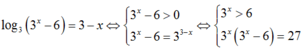
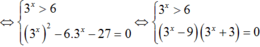
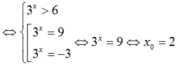
Mà x0 là nghiệm của phương trình log3( x + 7a) = 2log2x nên suy ra
log3( x + 7a) = 2log2x tương đương log3( x +7a) = 2
do đó; 7a + 2 = 32
suy ra a = 1.

Đáp án C
Mệnh đề (I) đúng.
Mệnh đề (II) sai vì log3 x2 = 2log3 x > 0 khi x > 0 nên điều kiện ∀ x ∈ ℝ \ 0 chưa đủ.
Mệnh đề (III) sai vì loga (b.c) = loga b + loga c.
Số mệnh đề đúng là 1.

Đáp án D
Ta có
A = log 2017 + log 2016 + log 2015 + log ... + log 3 + log 2 ... > log 2017 + log 2016 > log 2017 + 3 = log 2010 ⇒ A > log 2010
Áp dụng bất đẳng thức log x < x , ∀ x > 1 , ta có
2015 + log 2014 + log ... + log 3 + log 2 ... < 2015 + 2014 + log ... + log 3 + log 2 ... < 2015+1014+2013+ ... +3+2= 2017 × 2014 2
Khi đó
log 2016 + log 2015 + log 2014 + log ... + log 3 + log 2 ... < log 2016 + 2017 × 2014 2 < 4
Vậy A < log 2017 + 4 = log 2021 → A ∈ log 2010 ; 2021

Đáp án D.
Dựa vào đáp án ta suy ra 3 < A < 4 .
⇒ 3 < log 2019 < A 2016 = log 2016 + A 2015 < log 2020 < 4
⇒ 3 < log 2020 < A 2017 = log 2017 + A 2016 < log 2021 < 4
Vậy A 2017 ∈ log 2020 ; log 2021 .
Đáp án A