Cho hàm số y = x 3 + a x 2 + b x + c b < 0 . Biết rằng đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt đối xứng qua gốc tọa độ. Giá trị của T=2(ab-c)+3 là:
A. T=3
B. T=1
C. T=2
D. T=5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
20 tháng 11 2017
Đúng(0)
Những câu hỏi liên quan
CM
29 tháng 12 2019
Đáp án D
Trên khoảng ( a ; b ) và ( c ; + ∞ ) hàm số đồng biến vì y'>0 đồ thị nằm hoàn toàn trên trục Ox
Hàm số nghịch biến trên các khoảng ( - ∞ ; a ) và (b;c) vì y'<0
Suy ra x=b là điểm cực đại mà y(b) <0 do đó trục hoành cắt đồ thị tại hai điểm phân biệt. Với d<0 ta có
MD
12 tháng 12 2023
y=3x+b
a)Vì hàm số cắt trục tung tại điểm có tung độ = -2 nên x=0,y=-2
Thay x=0,y=-2 vào hàm số ta đc:
3.0+b=-2
\(\Rightarrow\)b=-2
b)Để đồ thị hàm số đi qua điểm M[ -2, 1] nên x=-2,y=1
2.(-2)+b=1\(\Rightarrow\)-4+b=1\(\Rightarrow\)b=5
c) thay x=3,y=x-2 ta đc :
y=1-2=-1
Thay x=1 và y=-1 vào y=3x+b ta đc
3.1+b=-1 \(\Rightarrow\)3+b=-1 \(\Rightarrow\)b=-4
20 tháng 12 2022
a: Để (d)//Ox thì m-1=0
=>m=1
b: Thay x=-1 và y=1 vào (d), ta được:
-m+1+m=1
=>1=1(luôn đúng)
c: Thay x=\(\dfrac{2-\sqrt{3}}{2}\) và y=0 vào (d), ta đc:
\(\left(m-1\right)\cdot\dfrac{2-\sqrt{3}}{2}+m=0\)
=>\(\left(m-1\right)\cdot\left(2-\sqrt{3}\right)+2m=0\)
=>\(2m-\sqrt{3}m-2+\sqrt{3}+2m=0\)
=>\(m\left(4-\sqrt{3}\right)=2-\sqrt{3}\)
=>\(m=\dfrac{2-\sqrt{3}}{4-\sqrt{3}}\)
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Lời giải:
a. Vì đths đi qua $A(-2;3)$ nên:
$y_A=(2m+5)x_A-1$
$\Rightarrow 3=(2m+5)(-2)-1\Rightarrow m=\frac{-7}{2}$
b. ĐTHS sau khi tìm được $m$ có pt: $y=-2x-1$. Bạn có thể tự vẽ
c. ĐTHS cắt trục hoành tại điểm có hoành độ -3, tức là đi qua điểm $(-3,0)$
$\Rightarrow 0=(2m+5)(-3)-1$
$\Rightarrow m=\frac{-8}{3}$
4 tháng 10 2021
1: Để hàm số đồng biến thì m-3>0
hay m>3
2: Thay x=0 và y=0 vào (d), ta được:
3m+7=0
hay \(m=-\dfrac{7}{3}\)
CM
7 tháng 1 2017
Đáp án B
Giả thiết
Đặt
thì
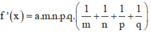
Và
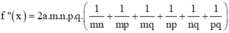
Khi đó, phương trình
(vô nghiệm)
Vậy đồ thị hàm số y = g(x) không cắt trục hoành.
CM
3 tháng 4 2018
Ta có
Đồ thị hàm số 
cắt trục hoành tại bốn điểm phân biệt bên phương trình 
, với 
là các nghiệm.
Suy ra
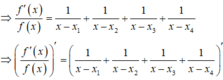
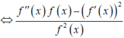
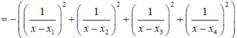
Nếu 
với 
thì 
, 
.
Nếu 
thì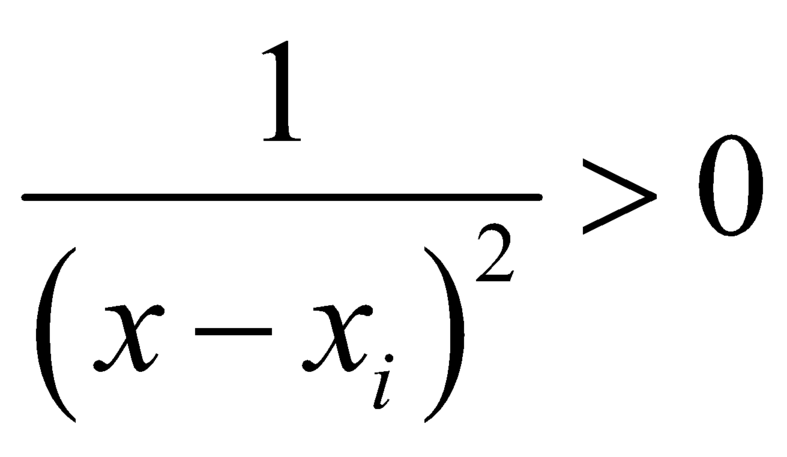 
, 
.
Suy ra 
.
Vậy phương trình 
vô nghiệm hay phương trình 
vô nghiệm.
Do đó, số giao điểm của đồ thị hàm số và trục hoành là 0
Đáp án A