Một cấp số nhân lùi vô hạn có tổng bằng S. Biết số hạng thứ hai của cấp số nhân đó bằng 1. Tìm giá trị nhỏ nhất có thể của S
A. 1 + 5 2
B. 3
C. 4
D. 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2022
\(\dfrac{u_1}{1-q}=2\Rightarrow q=\dfrac{2-u_1}{2}\)
\(u_1+u_1q+u_1q^2=\dfrac{9}{4}\)
\(\Rightarrow u_1+\dfrac{u_1\left(2-u_1\right)}{2}+\dfrac{u_1\left(2-u_1\right)^2}{4}=\dfrac{9}{4}\)
\(\Rightarrow u_1^3-6u_1^2+12u_1-9=0\)
\(\Rightarrow u_1=3\)
PT
1
CM
19 tháng 6 2019
a) Cấp số nhân vô hạn với công bội q mà |q| < 1 là cấp số nhân lùi vô hạn
b) Ví dụ về cấp số nhân lùi vô hạn có công bội âm:
21 tháng 4 2016
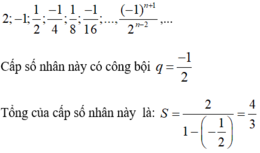
Theo giả thiết ta có :
\(u_1+u_2=u_1+\frac{1}{4}\left(u_1\right)=24\)
\(\Rightarrow u_1+\frac{1}{4}u_1^2-24=0\)
\(\Leftrightarrow u_1=-12\) V \(u_1=8\)
Vậy có 2 cấp số nhân tương ứng là : 8,16,32,128 hoặc -12,36,-108,-972
Đáp án C.
Gọi q là công sai của cấp số nhân. Vì u 2 = 1 nên suy ra u 1 = u 2 q = 1 q .
Ta có
S = u 1 1 − q = 1 q 1 − q = 1 q 1 − q , q < 1
Ta có a − b 2 ≥ 0 ⇔ a 2 + b 2 ≥ 2 a b ⇔ a + b 2 4 ≥ a b (với mọi a ; b ∈ ℝ ).
Áp dụng bất đẳng thức vừa chứng minh ở trên ta có q 1 − q ≤ q + 1 − q 2 4 = 1 4 ⇔ 1 q 1 − q ≥ 4 ⇔ S ≥ 4
Dấu bằng xảy ra khi q = 1 2 .
Vậy giá trị nhỏ nhất của S là 4 khi q = 1 2 .