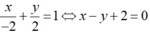Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x-y+2=0 Viết phương trình đường thẳng d’ là ảnh của d qua phép quay tâm O góc quay - 90 ∘
A. d' : x+3y+2=0
B. d' : x+3y-2=0
C. d' : 3x-y-6=0
D. C. d' : x-3y-2=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B
d cắt Ox,Oy lần lượt tại A − 3 ; 0 ; B 0 ; − 3 2 Qua phép quay tâm O góc quay − 90 ° điểm A và B lần lượt biến thành các điểm A ' 0 ; 3 ; B − 3 2 ; 0 ⇒ A ' B ' : 2 x − y + 3 = 0
Phép vị tự biến đường thẳng thành đường thẳng song song với nó nên d ' : 2 x − y + m = 0
Qua V O ; k A ' = A 1 ⇒ O A 1 → = 5 O A ' → ⇒ A 1 0 ; 15 ⇒ d ' : 2 x − y + 15 = 0

Dễ thấy d chứa điểm H(1;1) và OH ⊥ d. Gọi H' là ảnh của H qua phép quay tâm O góc 45 o thì H ′ = ( 0 ; 2 ) . Từ đó suy ra d' phải qua H' và vuông góc với OH'. Vậy phương trình của d' là y = 2 .

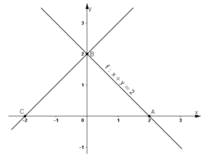
* Ta có A(2; 0) thuộc tia Ox.
Gọi Q(O,90º) (A) = B thì B thuộc tia Oy và OA = OB nên B(0 ; 2).
* Gọi d’ là ảnh của d qua phép quay tâm O, góc quay 90º.
+ A(2 ; 0) ∈ (d)
⇒ B = Q(O,90º) (A) ∈ (d’)
+ B(0 ; 2) ∈ (d).
⇒ C = Q(O,90º) (B) ∈ (d’).
Dễ dàng nhận thấy C(-2; 0) (hình vẽ).
⇒ (d’) chính là đường thẳng BC.
Đường thẳng d’ đi qua B(0 ; 2) và C(-2; 0) nên có phương trình đoạn chắn là: