Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)
ta có nghiệm của phương trình x2-1 là +1 vậy tổng nghiệm của pt này là 0
tiếp tục với x2-2 ngiệm pt này là +\(\sqrt{2}\)và -\(\sqrt{2}\) tổng hai ngiệm của pt này cũng bằng không
tương tự với x2-3 ,x2-4
-> tổng tất cả nghiệm của pt trên bằng 0
1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)
lập bảng xét dấu
x -3 2
x-2 - | - 0 +
x+3 - 0 + | +
Xét khoảng x<=3
=> |x-2|+|x+3|=5 <=> -x+2-x-3=5
<=> -3 (TM)
Xét khoảng -3<x<=2
=> |x-2|+|x+3|=5 <=> -x+2+x+3=5
<=> 0x=0 <=> x=-2;-1;0;1;2
Xét khoảng x>2
=> |x-2|+|x+3|=5 <=> x-2+x+3 =5
<=> x=0 (ko thỏa mãn)
Vậy X= -3;-2;-1;0;1;2
Ta xét các trường hợp sau:
+ TH1. x- 3= 1 hay x= 4. Khi đó; phương trình đã cho trở thành : 112= 1 luôn đúng.
=> x= 4 là nghiệm của phương trình.
+ TH2. .
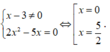
Vậy phương trình đã cho có ba nghiệm
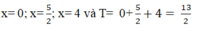
Chọn C.
