Cho hàm số
y
=
x
4
-
2
x
2
có đồ thị (C). Có bao nhiêu đường thẳng d có đúng ba điểm chung với đồ thị (C) và các điểm chung có hoành độ
x
1
,
x
2
,
x
3
thỏa mãn
x
1
3
+
x
2
3
+
x
3
3
=
-
1
? A. 0 B. 1 C. 2 D....
Đọc tiếp
Cho hàm số y = x 4 - 2 x 2 có đồ thị (C). Có bao nhiêu đường thẳng d có đúng ba điểm chung với đồ thị (C) và các điểm chung có hoành độ x 1 , x 2 , x 3 thỏa mãn x 1 3 + x 2 3 + x 3 3 = - 1 ?
A. 0
B. 1
C. 2
D. 3
Giả sử đường thẳng cần tìm có dạng y=kx+m. Phương trình hoành độ giao điểm:
x 4 - 2 x 2 = k x + m ⇔ x 4 - 2 x 2 - k x - m = 0
Theo giả thiết đường thẳng d có đúng ba điểm chung với đồ thị (C) và các điểm chung có hoành độ x 1 , x 2 , x 3 nên x 4 - 2 x 2 - k x - m = x - x 1 2 x - x 2 x - x 3 . Do đó d là tiếp tuyến của (C) có hoành độ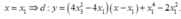
Phương trình hoành độ giao điểm lúc này là:
Yêu cầu bài toán tương đương với (1) có hai nghiệm phân biệt x 2 , x 3 # x 1
và x 1 3 + x 2 3 + x 3 3 = - 1
Vì vậy
Vì vậy có duy nhất một đường thẳng thoả mãn là tiếp tuyến tại điểm có hoành độ x = - 11 + 65 22 .
Chọn đáp án B.
*Chú ý dạng toán này thuộc bài học tiếp tuyến cắt đồ thị hàm số.