Cặp hàm số nào sau đây có tính chất: có một hàm số là nguyên hàm của hàm số còn lại
A. f x = sin 2 x và g x = cos 2 x .
B. f x = tan 2 x và g x = 1 cos 2 x .
C. f x = e x và g x = e − x .
D. f x = sin 2 x và g x = sin 2 x .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
F ' ( x ) = sin x - cos x ' sin x - cos x = cos x + sin x sin x - cos x

Chọn D.
Xét g(x) = f x 2 - 2
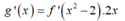
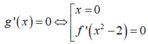
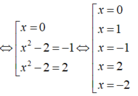
Bảng xét dấu g’(x):

Suy ra hàm số g(x) nghịch biến trên (-1;0) là sai.

Để kiểm tra một hàm F(x) có phải là một nguyên hàm của f(x) không thì ta chỉ cần kiểm tra F'(x) có bằng f(x) không?
a) \(F\left(x\right)\) là hằng số nên \(F'\left(x\right)=0\ne f\left(x\right)\)
b) \(G'\left(x\right)=2.\dfrac{1}{2}.\dfrac{1}{\cos^2x}=1+\tan^2x\)
c) \(H'\left(x\right)=\dfrac{\cos x}{1+\sin x}\)
d) \(K'\left(x\right)=-2.\dfrac{-\left(\dfrac{1}{2}.\dfrac{1}{\cos^2\dfrac{x}{2}}\right)}{\left(1+\tan\dfrac{x}{2}\right)^2}=\dfrac{\dfrac{1}{\cos^2\dfrac{x}{2}}}{\left(\dfrac{\cos\dfrac{x}{2}+\sin\dfrac{x}{2}}{\cos\dfrac{x}{2}}\right)^2}\)
\(=\dfrac{1}{\left(\cos\dfrac{x}{2}+\sin\dfrac{x}{2}\right)^2}=\dfrac{1}{1+2\cos\dfrac{x}{2}\sin\dfrac{x}{2}}\)
\(=\dfrac{1}{1+\sin x}\)
Vậy hàm số K(x) là một nguyên hàm của f(x).

Chọn D
Xét hàm số ![]() . Khi đó hàm số
. Khi đó hàm số ![]() liên tục trên các đoạn
liên tục trên các đoạn ![]() ,
, ![]() và có
và có ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() .
.
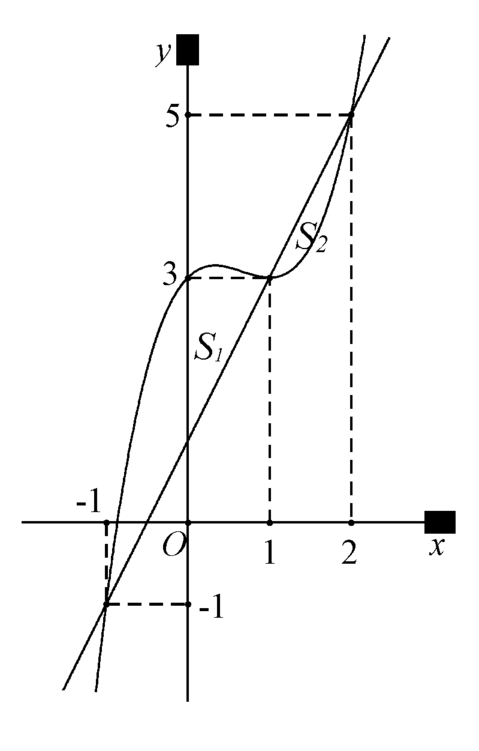
Do đó diện tích hình phẳng giới hạn bởi  là
là
![]()
![]()
![]()
![]() .
.
Vì ![]() nên
nên ![]() .
.
Diện tích hình phẳng giới hạn bởi 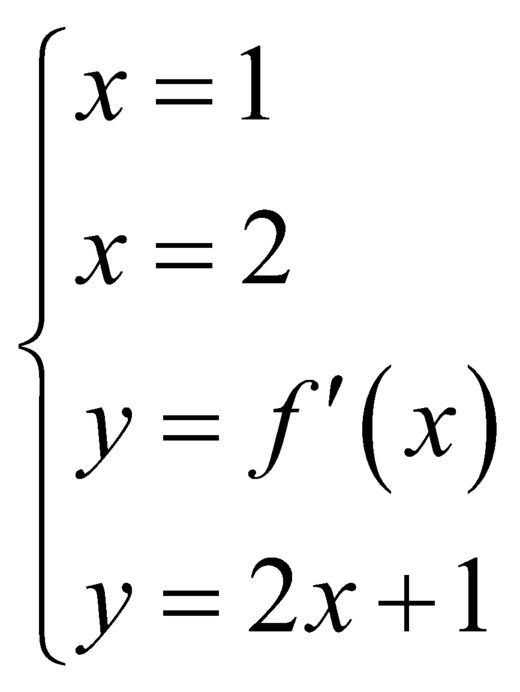 là
là
![]()
![]()
![]()
![]() .
.
Vì ![]() nên
nên ![]() .
.
Đáp án D
Với A: Ta có ∫ sin 2 x d x = ∫ 2. sin x . cos x d x = − ∫ 2 cos x d cos x (ta loại A).
Từ A ta xét D luôn có tính chất tương tự.
Với D: Ta có
∫ f x d x = ∫ sin 2 x . d x = ∫ 2 sin x . cos x d x = ∫ 2 sin x d sin x = sin 2 x = g x
Vậy ta chọn D.