Cho số phức z = 3 − 2 i . Tìm điểm biểu diễn của số phức w = z + i . z ¯
A. M 1 ; 1
B. M 1 ; − 5
C. M 5 ; − 5
D. M 5 ; 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 8 2019
Ta có : w - 1 + 2 i = z ⇔ w = z + 1 - 2 i . Suy ra quỹ tích các điểm biểu diễn số phức w có được từ quỹ tích các điểm biểu diễn số phức z bằng cách thực hiện phép tịnh tiến theo v → = ( 1 ; - 2 ) . Do đó quỹ tích quỹ tích các điểm biểu diễn số phức w là đường tròn tâm (-1;1) bán kính bằng 3.
Đáp án D
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2021
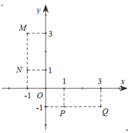
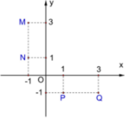
\(M\left(1;1\right)\) ; \(N\left(2;3\right)\)
Gọi \(w=x+yi\Rightarrow Q\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;2\right)\\\overrightarrow{MQ}=\left(x-1;y-1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MN}+3\overrightarrow{MQ}=\left(3x-2;3y-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow w=\dfrac{2}{3}+\dfrac{1}{3}i\)
CM
14 tháng 8 2019
Chọn đáp án D.
Phương pháp: Ta tìm số phức w biểu diễn ở dạng w=a+bi
Khi đó điểm biểu diễn số phức w là điểm có toạ độ (a;b).
Cách giải:
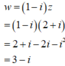
Vậy điểm biểu diễn số phức z có toạ độ (3;-1)
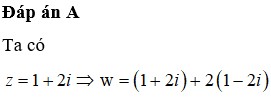
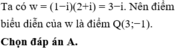
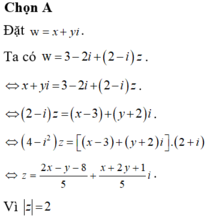
Đáp án A
Ta có z ¯ = 3 + 2 i ⇒ w − z + i z ¯ = 3 − 2 i + i 3 + 2 i = 1 + i ⇒ M 1 ; 1