Một vật dao động điều hòa trên trục Ox. Gọi t 1 v à t 2 lần lượt là khoảng thời gian ngắn nhất và dài nhất để vật đi được quãng đường bằng biên độ. Tỉ số t 1 / t 2 bằng
A. 2
B. 1 / 2
C. 1 / 3
D. 0 , 5 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để thời gian đi được ngắn nhất thì vận tốc phải lớn nhất.
Vận tốc lớn nhất khi vật ở lân cận VTCB.
Khoảng cách giữa -A/2 và A/2 là A và hai điểm này lân cận VTCB, thời gian ngắn nhất để đi từ VTCB đến chính giữa biên là T/12
→ t1=2*T/12=T/6
Tương tự, quãng đường đi có độ dài A mà trong lúc đi vận tốc của vật giảm dần đến nhỏ nhất là từ VTCB đến biên
→ t2=T/4
t1/t2= 2/3

\(\Delta\varphi=\omega\Delta t=2\left(rad\right)\) \(\Rightarrow\) \(\left\{{}\begin{matrix}\text{S}_{max}=2Asin\dfrac{\Delta\varphi}{\text{2}}=2.10sin1\approx\text{16,83(cm)}\\\text{S}_{\text{min}}=\text{2A}\left(\text{1-cos}\dfrac{\Delta\varphi}{\text{2}}\right)=2.10\left(\text{1-cos1}\right)\approx\text{9,19(cm)}\end{matrix}\right.\)
Tham khảo:
\(\Delta\varphi=\omega\Delta t=2\left(rad/s\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}S_{max}=2Asin\dfrac{\Delta\varphi}{2}=2\cdot10sin1\approx16,8\left(cm\right)\\S_{min}=2A\left(1-cos\dfrac{\Delta\varphi}{2}\right)=2\cdot10\cdot\left(1-cos1\right)\approx9,19\left(cm\right)\end{matrix}\right.\)

Đáp án D
+ Trong khoảng thời gian t = T/4 thì vật có thể chuyển động từ vị trí ±A ® VTCB hoặc từ VTCB ® ±A hoặc từ vị trí
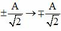
+ Smax khi vật đi từ
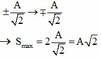

Đáp án D
Trong khoảng thời gian t = T 4 thì vật có thể chuyển động từ vị trí ±A ® VTCB hoặc từ VTCB ® ±A hoặc từ vị trí
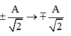

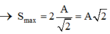
Đáp án B