Tổng bình phương giá trị lớn nhât và giá trị nhỏ nhât của hàm số y = x + 1 x 2 + 1 trên đoạn [0;3] là.
A.3
B.2
C.5
D.4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
6 tháng 11 2019
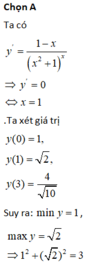
Ta có
y = 1 - x x 2 + 1 x ⇒ y = 0 ⇔ x = 1
Ta xét giá trị
y 0 = 1 , y 1 = 2 , y 3 = 4 10
Suy ra miny=1, maxy= 2
⇒ 1 2 + 2 2 = 3
Chọn đáp án A.
CM
8 tháng 7 2017
Đáp án C
Ta có: y ' = 4 x 3 − 4 x = 0 ⇔ 4 x x 2 − 1 = 0 ⇔ x = 0 x = ± 1
Mà y 0 = 3 ; y 1 = 2 ; y 2 = 11 ⇒ M = 11 , m = 2.
CM
13 tháng 8 2017
Đáp án C
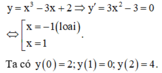
Vậy tổng bình phương giá trị lớn nhất và giá trị nhỏ nhất là 16.
CM
19 tháng 12 2018
Đáp án D
y = 2 cos x 2 + s i nx + 1 y ' = − sin x 2 + cos x = − 2 sin 2 x 2 − sin x 2 + 1 y ' = 0 ⇔ sin x 2 = − 1 sin x 2 = 1 2 ⇔ x 2 = − π 2 + k 2 π x 2 = π 6 + k 2 π x 2 = 5 π 6 + k 2 π ⇔ x = − π + k 4 π x = π 3 + k 4 π x = 5 π 3 + k 4 π y ( − π ) = 1 y ( 0 ) = 3 y ( π 3 ) = 2 + 3 3 2 y ( 5 π 3 ) = 2 − 3 3 2 y ( π ) = 1 ⇒ min y = 2 − 3 3 2
DD
0