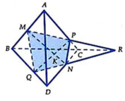
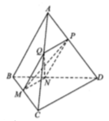
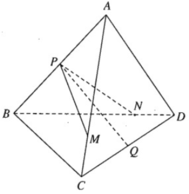
Cho tứ diện ABCD và M, N là các điểm thay đổi trên cạnh AB và CD sao cho A M M B = C N N D . Gọi P là một điểm trên cạnh AC và S là diện tích thiết diện cắt bởi mặt phẳng M N P và hình chóp. Tính tỉ số k của diện tích tam giác MNP và diện tích thiết diện S.
A. 2 k k + 1 .
B. 1 k .
C. k k + 1 .
D. 1 k + 1 .




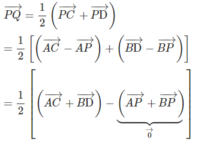
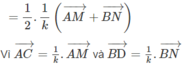
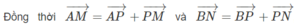
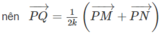
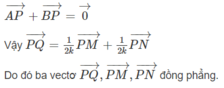
Đáp án C
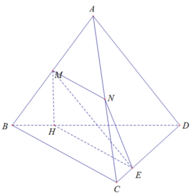
Xét trường hợp A P P C = k , lúc này M P // B C nên B C // M N P .
Ta có: N ∈ M N P ∩ B C D B C // M N P B C ⊂ B C D ⇒ B C D ∩ M N P = N Q // B C , Q ∈ B D .
Thiết diện là tứ giác MPNQ.
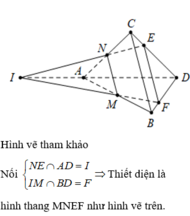
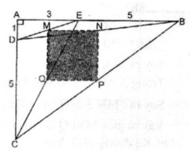
Xét trường hợp A P P C ≠ k .
Trong A B C gọi R = B C ∩ M P .
Trong B C D gọi Q = N R ∩ B D thì thiết diện là tứ giác MNPQ.
Gọi K = M N ∩ P Q . Ta có S M N P S M N P Q = P K P Q .
Do A M N B = C N N D nên theo định lí Thales đảo thì A C , N M , B D lần lượt thuộc ba mặt phẳng song song với nhau và đường thẳng PQ cắt ba mặt phẳng này tương ứng tại P, K, Q nên áp dụng định lí Thales ta được P K K Q = A M M B = C N N D = k
⇒ P K P Q = P K P K + K Q = P K K Q P K K Q + 1 = k k + 1