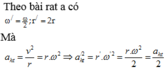Gia tốc hướng tâm của chuyển động tròn đều tăng hay giảm bao nhiêu nếu vận tốc góc giảm còn một nửa nhưng bán kính quỹ đạo tăng 2 lần
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VT
Vũ Thành Nam
28 tháng 9 2017
Đúng(0)
Những câu hỏi liên quan
VT
30 tháng 4 2017
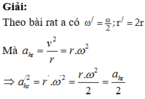
Chọn đáp án A
+ Theo bài ra ta có ω ' = 2 ω , r ' = 2 r
+ Mà
MH
17 tháng 10 2021
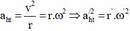
sau 20 s vật quay được 10 vòng
⇒ 1s vật quay được 0,5 vòng
⇒ f = 0,5 vòng/s
ta có \(T=\dfrac{1}{f}=\dfrac{1}{0,5}=2s\)
b, đổi 20cm = 0,2 m
\(T=\dfrac{2\text{π}}{\text{ω}}\)⇒ω\(=\dfrac{2\text{π}}{T}\)\(=\dfrac{2\text{π}}{2}\)\(=\text{π}\) rad/s
\(v=r\text{ω}\)\(=0,2\text{π}\)
c, \(a_{ht}=\dfrac{v^2}{r}=\dfrac{0,4\text{π}^2}{0,2}=0,2\text{π}^2\)
: …………. (rad/s).
=0,04 m/s2. Chu kì T chuyển động của vật đó bằng bao nhiêu? Lấy π = 3,14
N
9 tháng 12 2021
Ta có: \(f=\dfrac{n}{t}=\dfrac{100}{2}=50\left(Hz\right)\)
\(=>\omega=\dfrac{2\pi}{f}=\dfrac{2\pi}{50}=\dfrac{1}{25}\pi\left(\dfrac{rad}{s}\right)\)
\(=>v=\pi r=\dfrac{1}{25}\pi\cdot0,5=\dfrac{1}{50}\pi\left(\dfrac{m}{s}\right)\)
\(=>a_{huongtam}=\dfrac{v^2}{r}=\dfrac{\left(\dfrac{1}{50}\pi\right)^2}{0,5}=\dfrac{1}{1250}\pi^2\left(\dfrac{rad^s}{s}\right)\)