Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh SA vuông góc với đáy và SA=y Trên cạnh AD lấy điểm M sao cho AM=x Biết rằng x 2 + y 2 = a 2 Tìm giá trị lớn nhất của thể tích khối chóp S.ABCM.

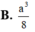
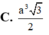
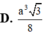
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
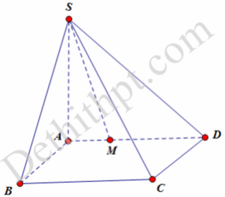
Ta có
V = 1 3 S A . S A B C M = 1 3 y . 1 2 a x + a = 1 6 a x + a a 2 − x 2
Xét f x = x + a a 2 − x 2
⇒ f ' x = a 2 − x 2 + x + a . − x a 2 − x 2 = 0
⇒ a 2 − x 2 = x x + a ⇔ 2 x 2 + a x − a 2 = 0 ⇔ x + a 2 x − a = 0 ⇔ x = a 2
⇒ V ≤ 1 6 a a 2 + a a 2 − a 2 2 = a 3 3 8

Đáp án B
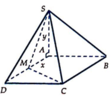
S A = y = a 2 - x 2 ; S A B C M = B C + A M 2 . A B = a + x 2 . a
S A B C M = 1 3 S A B C M . S A = a 6 ( a + x ) a 2 - x 2
Xét hàm số f ( x ) = ( a + x ) a 2 - x 2 trên 0 ; a ta được:
m a x 0 ; a f ( x ) = f a 2 = 3 3 a 2 4 ⇒ V m a x = a 3 3 8

Đáp án B
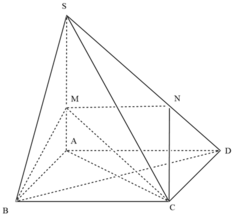
Kẻ MN // AD // AD nên (MBC) cắt (SAD) theo giao tuyến là MN

