Cho điểm I(x, y) trên mặt phẳng tọa độ và số thực R. Vẽ trên màn hình đường tròn tâm I, bán kính R.
Hãy cho biết input của bài toán là gì?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

#include <bits/stdc++.h>
using namespace std;
double x,y,r,a,b;
int main()
{
cin>>x>>y>>r>>a>>b;
im=sqrt((x-a)*(x-a)+(y-b)*(y-b));
if (im==r) cout<<"Diem M nam tren duong tron";
else cout<<"Diem M khong nam tren duong tron";
return 0;
}

Gọi I a ; - a a > 0 thuộc đường thẳng y = - x
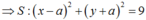
(S) tiếp xúc với các trục tọa độ
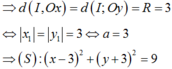
Chọn B.

2:
#include <bits/stdc++.h>
using namespace std;
double xm,ix,iy,r,ma,mb;
int main()
{
cin>>ix>>iy;
cin>>r;
cin>>ma>>mb;
xm=sqrt((ix-ma)*(ix-ma)+(iy-mb)*(iy-mb));
if (xm==r) cout<<"phai";
else cout<<"khong phai";
return 0;
}

Đáp án D.
Phương pháp:
Gọi z = a + b i , sử dụng công thức tính môđun của số phức.
Cách giải:
Giả sử z = x + y i , x , y ∈ R
Theo đề bài ta có:
z + 3 − 4 i = 5 ⇔ x + 3 2 + y − 4 2 = 5 ⇔ x + 3 2 + y − 4 2 = 25
Vậy, tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là đường tròn tâm I − 3 ; 4 , R = 5.

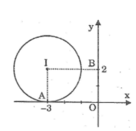
Kẻ IA ⊥ Ox
Ta có: IA = 2 = R
Suy ra đường tròn (I) tiếp xúc với trục hoành
Kẻ IB ⊥ Oy
Ta có : IB = 3 > R
Suy ra đường tròn và trục tung không có điểm chung
Input: xi,yi,R