Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a, A B C ⏜ = 60 0 . Gọi O là tâm của hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng
A. 5 a 4
B. 3 a 8
C. 5 a 8
D. 3 a 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

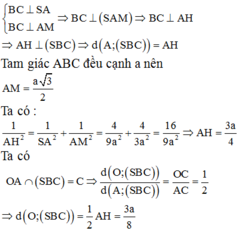

Chọn đáp án B.
Ta có: 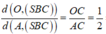
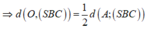
Vì AB = BC = a, ![]()
Gọi M là trung điểm BC.
Do đó: 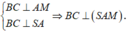
Gọi H là hình chiếu của A lên SM.
Do đó:
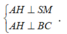
![]()
Xét tam giác SAM vuông tại A:
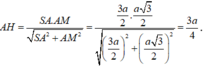
Vậy ![]()

Đáp án B.
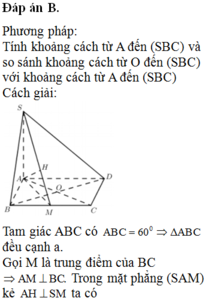
Phương pháp: Tính khoảng cách từ A đến (SBC) và so sánh khoảng cách từ O đến (SBC) với khoảng cách từ A đến (SBC)
Cách giải: Tam giác ABC có góc ABC = 600 => ∆ABC đều cạnh a.
Gọi M là trung điểm của BC => AM ⊥ BC. Trong mặt phẳng (SAM) kẻ AH ⊥ SM ta có
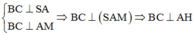
![]()
Tam giác ABC đều cạnh a nên 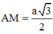
Ta có : 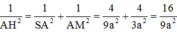
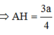
Ta có ![]()
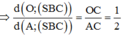
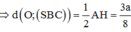
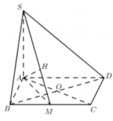

Đáp án C
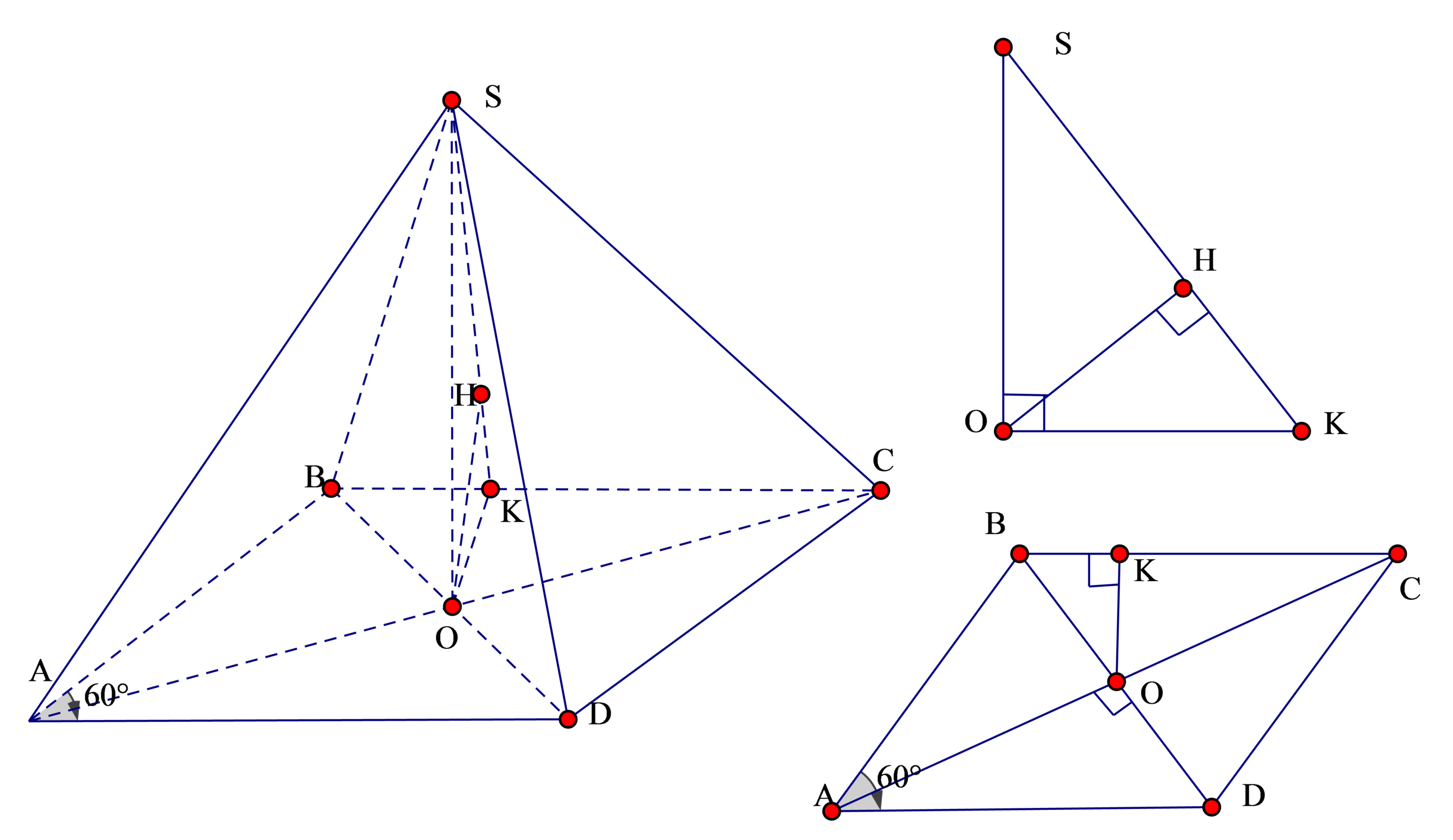
Kẻ O K ⊥ B C , O H ⊥ S K như hình vẽ khi đó OH là khoảng cách từ O tới (SBC)
Dễ thấy Δ A B D đều
⇒ O K = O B . sin 60 0 = a 2 . 3 2 = a 3 4
Ta có: 1 O H 2 = 1 O K 2 + 1 S O 2 = 16 3 a 2 + 1 a 2 = 19 3 a 2
⇒ O H = a 57 19