Giả sử x, y là những số thực dương thỏa mãn: log 16 x + y = log 9 x = log 12 y . Tính giá trị của biểu P = 1 + x y + x y 2
A. P = 16
B. P = 2
C. P = 3 + 5 2
D. P = 3 + 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có log(x + 2y) = log x + log y
<=> log 2 (x+2y) = log 2xy
<=> 2 (x+2y) = 2xy (*).
Đ ặ t a = x > 0 b = 2 y > 0 , khi đó
* ⇔ 2 a + b = a b
và P = a 2 1 + b + b 2 1 + a ≥ a + b 2 a + b + 2
Lại có a b ≤ a + b 2 4 ⇒ 2 a + b ≤ a + b 2 4 ⇔ a + b ≥ 8 .
Đặt t = a + b, do đó
P ≥ f t = t 2 t + 2 .
X é t h à m s ố f t = t 2 t + 2 t r ê n [ 8 ; + ∞ )
c ó f ' t = t 2 + 2 t t + 2 2 > 0 ; ∀ ≥ 8
Suy ra f(t) là hàm số đồng biến trên [ 8 ; + ∞ )
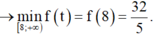
Vậy gía trị nhỏ nhất của biểu thức P là 32 5 .

a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)
Với \(x = 2\) thì \(y = {\log _2}2 = 1\)
Với \(x = 4\) thì \(y = {\log _2}4 = 2\)
b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.
Đáp án B
log 16 x + y = log 9 x = log 12 y = t ⇒ 16 t = x + y 9 t = x 12 t = y ⇒ x y = 9 t 12 t = 3 4 t 16 t 12 t = 4 3 t = x y + 1
⇒ x y = 3 4 t = 1 x y + 1 ⇔ x y 2 + x y = 1 = P − 1 ⇔ P = 2.