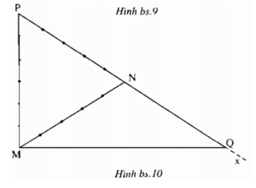
Tam giác MNP có MP = 6cm, MN = PN = 5cm. Góc MNx kề bù với góc MNP. Điểm Q trên tia Nx sao cho NQ = NM (h.bs.10). Khi đó, độ dài của đoạn thẳng PQ bằng
(A) 5;
(B) 6;
(C) 8;
(D) 10.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Giải thích
Góc MNX kề bù với góc MNP
=>Tia Nx,tia NP đối nhau
mà điểm Q thuộc tia Nx
=>Tia NQ ,tia NP đối nhau
=>Điểm N nằm giữa 2 điểm Q,P
=>NQ+NP=PQ (1)
mà NQ=NM,NM=NP=5(cm)
=>NQ=NP=5(cm) (2)
Từ (1) và (2)
=>PQ=5+5
=>PQ=10(cm)

cho tam giác MNP vuông tại M có MN=4cm;MP=3cm
a)tính đọ dài NP và so sánh các góc của tam giác MNP
b)Trên tia đối tia PM lấy A sao cho P là trung điểm của đoạn thẳng AM.QUa P dựng đường thẳng vuông góc với AM cắt AN tại C.C/m tam giác CPM=tam giác CPA
c)C/m CM=CN
d)GỌi G là giao điểm của MC và NP.TÍnh NG
e)Từ A vẽ đường thẳng vuông góc với NP tại D.Vẽ tia Nx là tia phân giác của góc MNP,vẽ tia Ay là tian pg của PAD,tia Ay cắt các tia NP,Nx,NM lần lượt tại E,H,K.C/m tam giác NEK cân

a: Xét ΔMNI và ΔMPI có
MN=MP
NI=PI
MI chung
Do đó: ΔMNI=ΔMPI
Ta có: ΔMNP cân tại M
mà MI là đường trung tuyến
nên MI là đường cao
b: Xét tứ giác MNQP có
I là trung điểm của MQ
I là trung điểm của NP
Do đó: MNQP là hình bình hành
Suy ra: MN//PQ
c: Xét tứ giác MEQF có
ME//QF
ME=QF
Do đó: MEQF là hình bình hành
Suy ra: MQ và EF cắt nhau tại trung điểm của mỗi đường
mà I là trung điểm của MQ
nên I là trung điểm của FE
hay E,I,F thẳng hàng
Đáp án D