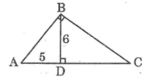
Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD bằng 5. Tính diện tích tam giác ABD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
4 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
18 tháng 9 2016
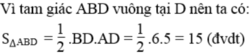
tinh ab bang pitago .su dung tam giac dong dang abd va abc suy ra ab2 =ad*ac the so roi tinh
10 tháng 9 2020
a) Vì tam giác ABD vuông tại D nên ta có:
SΔABD=12.BD.AD=12.6.5=15 (đvdt)
b) Ta có: tgˆC=BD/DC
Theo giả thiết: tgˆC=3/4
Suy ra: BD/DC=34⇒DC=4/3BD=4.6/3=8
Suy ra: AC=AD+DC=5+8=13 b a d c 5 6
11 tháng 9 2020
a) Vì tam giác ABD vuông tại D nên ta có:
SΔABD=12.BD.AD=12.6.5=15(đvdt)
b) Ta có: tgˆC=BD/DCt
Theo giả thiết: tgˆC=3/4
Suy ra: BD/DC=3/4⇒DC=4/3 BD=4.6/3=8 A B C 6 5
Suy ra: AC=AD+DC=5+8=13.
26 tháng 6 2021
a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
b) Ta có: ΔADB\(\sim\)ΔAEC(cmt)
nên \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔAED và ΔACB có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)(cmt)
\(\widehat{A}\) chung
Do đó: ΔAED\(\sim\)ΔACB(c-g-c)
10 tháng 12 2023
a: Xét ΔABC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{12}=\dfrac{CD}{14}\)
=>\(\dfrac{AD}{6}=\dfrac{CD}{7}\)
mà AD+CD=AC=9cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{7}=\dfrac{AD+CD}{6+7}=\dfrac{9}{13}\)
=>\(AD=\dfrac{9}{13}\cdot6=\dfrac{54}{13}\left(cm\right);CD=\dfrac{9}{13}\cdot7=\dfrac{63}{13}\left(cm\right)\)
b: Sửa đề: b) Tính tỉ số diện tích của tam giác ABD và tam giác BDC
Vì \(\dfrac{AD}{6}=\dfrac{CD}{7}\)
nên \(\dfrac{AD}{CD}=\dfrac{6}{7}\)
=>\(\dfrac{S_{ABD}}{S_{CBD}}=\dfrac{6}{7}\)
=>\(S_{ABD}=\dfrac{6}{7}\cdot S_{CBD}\)