Cho a, b là các số thực thuộc khoảng và thỏa mãn điều kiện .Tính giá trị của biểu thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(a^3+b^3\right)\left(a+b\right)=ab\left(1-a\right)\left(1-b\right)\)
\(\Leftrightarrow\left(1-a\right)\left(1-b\right)=\left(\dfrac{a^2}{b}+\dfrac{b^2}{a}\right)\left(a+b\right)\ge\left(a+b\right)^2\ge4ab\)
\(\Rightarrow1+ab-4ab\ge a+b\ge2\sqrt{ab}\)
\(\Rightarrow3ab+2\sqrt{ab}-1\le0\)
\(\Leftrightarrow\left(\sqrt{ab}+1\right)\left(3\sqrt{ab}-1\right)\le0\)
\(\Leftrightarrow ab\le\dfrac{1}{9}\)

Đáp án D
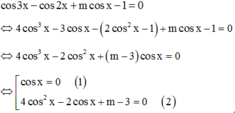
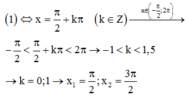
→
(1) có 2 nghiệm thuộc 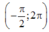
Để phương trình có đúng 8 nghiệm thuộc khoảng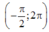 thì (2) phải có đúng 6 nghiệm phân biệt thuộc
thì (2) phải có đúng 6 nghiệm phân biệt thuộc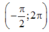 và khác
x
1
;
x
2
và khác
x
1
;
x
2
Đặt t = cos x ( - 1 ≤ x ≤ 1 ) , (2) trở thành f ( t ) = 4 t 2 - 2 t + m - 3 = 0 ( 3 )
+ Nếu
0
<
t
<
1
thì phương trình cosx=t có 3 nghiệm phân biệt thuộc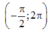
+ Nếu
-
1
<
t
<
0
thì phương trình cosx=t có 2 nghiệm phân biệt thuộc khoảng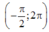
Do đó (2) có đúng 6 nghiệm phân biệt thuộc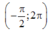
⇔ (3) có 2 nghiệm t 1 ; t 2 thỏa mãn 0 < t 1 < t 2 < 1
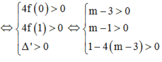


Đáp án A
Đặt t = log 3 2 x + 1 ⇒ t ' = log 3 x log 3 2 x + 1 . 1 x ln 3 ≥ 0 ∀ x ∈ 1 ; 3 2 2
Suy ra t ∈ 1 ; 3 : P T : t 2 + t - 2 - 5 m = 0 ⇔ t 2 + t - 2 = 5 m
Xét f t = t 2 + t - 2 , t ∈ 1 ; 3 ⇒ f ' t = 2 t + 1 > 0 nên hàm số đồng biến trên [1;3]
Do đó để phương trình có nghiệm thì 5 m ∈ f 1 ; f 3 ⇒ m ∈ 0 ; 2

\(a=-2b-5c\Rightarrow a+2b=-5c\)
- Với \(c=0\Rightarrow a=-2b\Rightarrow-\dfrac{b}{a}=\dfrac{1}{2}\)
\(ax^2+bx=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{b}{a}=\dfrac{1}{2}\in\left(0;1\right)\end{matrix}\right.\) (thỏa mãn)
- Với \(c\ne0\)
Hàm \(f\left(x\right)=ax^2+bx+c\) liên tục trên R
\(f\left(0\right)=c\) ;
\(f\left(\dfrac{1}{2}\right)=\dfrac{a}{4}+\dfrac{b}{2}+c=\dfrac{a+2b+4c}{4}=\dfrac{-5c+4c}{4}=-\dfrac{c}{4}\)
\(\Rightarrow f\left(0\right).f\left(\dfrac{1}{2}\right)=-\dfrac{c^2}{4}< 0;\forall c\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\dfrac{1}{2}\right)\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) do \(\left(0;\dfrac{1}{2}\right)\subset\left(0;1\right)\)

Để A hợp B=A thì B là tập con của A
=>2m-5<23 và 23<=-m
=>2m<28 và -m>=23
=>m<=-23 và m<14
=>m<=-23
=>Chọn B


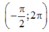 . Tính tổng T=a+b
. Tính tổng T=a+b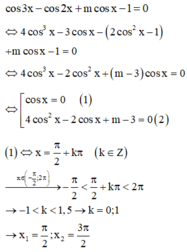


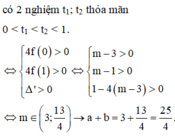
Đáp án A