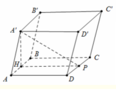
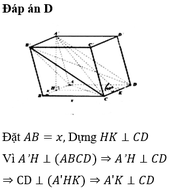
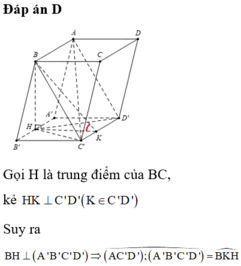
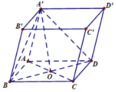
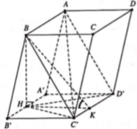
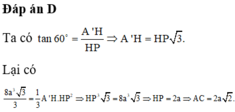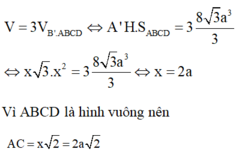Cho khối lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình vuông. Hình chiếu vuông góc của A' trên mặt phẳng (ABCD)là trung điểm của AB, góc giữa mặt phẳng (A'CD) và mặt phẳng (ABCD) là
60
O
Thể tích của khối chóp B'.ABCD là 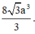 Tính độ dài đoạn thẳng AC.
Tính độ dài đoạn thẳng AC.
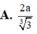
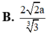
![]()
![]()