Cho tam giác cân ABC có đường cao A H = a 3 , B C = 3 a ,BC chứa trong mặt phẳng (P). Gọi A’ là hình chiếu vuông góc của A lên mặt phẳng (P). Biết tam giác A’BC vuông tại A’. Gọi j là góc giữa (P) và (ABC). Chọn khẳng định đúng trong các khẳng định sau?
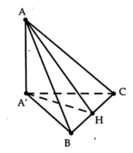
A. φ = 30 o
B. φ = 45 o
C. cos φ = 2 3
D. φ = 60 o

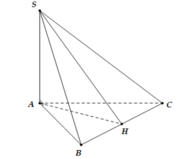
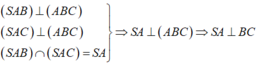
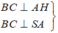
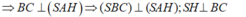
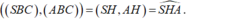




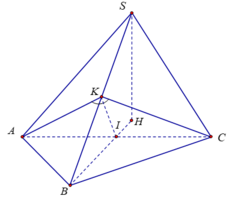
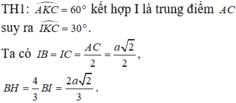
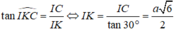
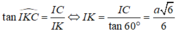
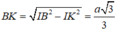
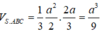
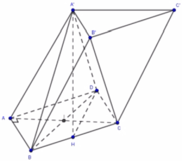
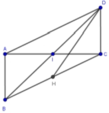
Đáp án D
Ta có: B C ⊥ A A ' B C ⊥ A H
Do đó:
Mặt khác, tam giác A’BC vuông cân tại A’
nên A ' H = 1 2 B C = 3 a 2
Ta có:
⇒ φ = 60 o