Tìm x thỏa mãn điều kiện: 4 x + 3 x + 1 = 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
19 tháng 10 2019
Đúng(0)
Những câu hỏi liên quan
TP
1
ND
Nguyễn Đức Trí
VIP
29 tháng 8 2023
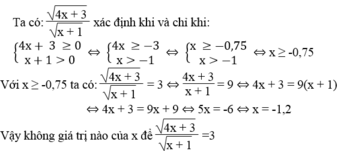
\(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|+\left|x+4\right|=5x\left(1\right)\)
Ta có :
\(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|+\left|x+4\right|\ge\left|x+1+x+2+x+3+x+4\right|=\left|4x+10\right|\)
\(pt\left(1\right)\Leftrightarrow\left|4x+10\right|=5x\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+10=5x\\4x+10=-5x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=10\\9x=-10\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-\dfrac{10}{9}\end{matrix}\right.\) \(\left(thỏa.mãnx\inℚ\right)\)
HE
1
HE
1
29 tháng 1 2022
\(\dfrac{1}{5}+\dfrac{2}{7}-1< x< \dfrac{13}{3}+\dfrac{6}{5}+\dfrac{4}{15}\)
\(\Leftrightarrow\dfrac{7}{35}+\dfrac{10}{35}-\dfrac{35}{35}< x< \dfrac{65}{15}+\dfrac{18}{15}+\dfrac{4}{15}\)
\(\Leftrightarrow\dfrac{-18}{35}< x< \dfrac{29}{5}\)
\(\Leftrightarrow\dfrac{-18}{35}< \dfrac{35x}{35}< \dfrac{203}{35}\)
\(\Leftrightarrow-18< 35x< 203\)
\(\Leftrightarrow x\in\left\{0;1;2;3;4;5\right\}\)
DT
0
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
Không em, phải thỏa cả ĐKXĐ ban đầu chứ
Do đó \(x=-2\) \(\Rightarrow A=-1\) mới là GTNN của A
10 tháng 12 2021
a: \(P=\dfrac{x^2+6x+9-x^2+6x-9-4}{\left(x-3\right)\left(x+3\right)}:\dfrac{3x-1}{x-3}\)
\(=\dfrac{4\left(3x-1\right)}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x-3}{3x-1}=\dfrac{4}{x+3}\)
TH
1
DT
30 tháng 4 2021
x + y = 1 => y = 1 - x
A = x3 + y3 = (x + y)(x2 - xy + y2)
= x2 - x(1 - x) + (1 - x)2
= x2 - x + x2 + x2 - 2x + 1
= 3x2 - 3x + 1
= 3(x2 - x + \(\dfrac{1}{3}\))
= 3(x2 - 2x.\(\dfrac{1}{2}\) + \(\dfrac{1}{4}+\dfrac{1}{12}\))
= 3(x - \(\dfrac{1}{2}\))2 + \(\dfrac{1}{4}\) ≥ \(\dfrac{1}{4}\) ∀x
Dấu "=" xảy ra ⇔ x - \(\dfrac{1}{2}\) = 0 ⇔ x = \(\dfrac{1}{2}\)
Vậy minA = \(\dfrac{1}{4}\) ⇔ x = \(\dfrac{1}{2}\)