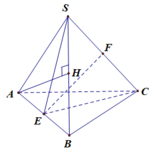
Cho hình chóp S.ABC với AB = SA = a, tất cả các cạnh còn lại bằng b. Độ dài EF (E, F là trung điểm của AB, SC) theo a, b
A. b 2 2
B. a 2 + 4 b 2 2
C. b 3 2
D. a 2 + 3 b 2 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(SA\perp BC\), \(AB\perp BC\) \(\Rightarrow SB\perp BC\)
Do đó : góc giữa 2 mặt phẳng (SBC) và (ABC) bằng \(\widehat{SBA}=30^0\)
\(V_{S.ABM}=\frac{1}{2}V_{S.ABC}=\frac{1}{2}SA.AB.BC\)
\(BC=AB=a;SA=AB.\tan30^0=\frac{a\sqrt{3}}{3}\)
Vậy \(V_{s.ABM}=\frac{a^3\sqrt{3}}{36}\)


Do đó, \(SD=\dfrac{a^2}{2}:a\sqrt{2}=\dfrac{a\sqrt{2}}{4}\)
và \(AD=SA-SD=\dfrac{3a\sqrt{2}}{4}\)

Đáp án B
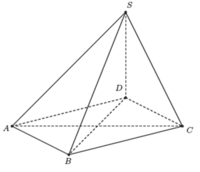
Gọi D là hình chiếu của S trên (ABC). Khi đó S D ⊥ A B C .
Do đó hình chiếu của SC trên (ABC) là CD. Suy ra góc giữa SC và (ABC) là S C D ^ .
Ta có B C ⊥ S C B C ⊥ S D ⇒ B C ⊥ C D , A B ⊥ S A A B ⊥ S D ⇒ A B ⊥ A D .
Vậy ABCD là hình chữ nhật.
Theo đề S C D ^ = 60 0 . Ta tính được B D = A C = a 5 , D S = C D 3 = a 3 .
Vậy S B = S D 2 + B D 2 = 8 a 2 = 2 a 2 .
Đáp án A
Áp dụng công thức trung tuyến ta có:
Theo Định lý PiTaGo ta có:
⇒ E F = 2 b 2