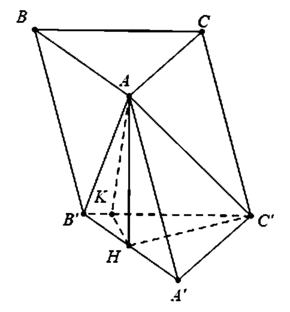
Cho lăng trụ ABC.A'B'C' có đáy là tam giác vuông tại A, AB = a và AC = a 2 . Biết rằng ((ABC),(AB'C')) = 60 ∘ và hình chiếu A lên (A'B'C') là trung điểm H của A'B'. Tính bán kính R của mặt cầu ngoại tiếp tứ diện AHB'C'.
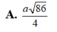
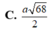
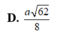
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Do góc giữa hai mặt phẳng (AB'C') và (ABC) bằng 60 °
Suy ra A B ' C ' ; A B C ^ = 60 °
Dựng H K ⊥ B ' C ' , do A H ⊥ B ' C ' ⇒ B ' C ' ⊥ A K H
Do đó A K H ^ = 60 °
 Mặt khác
B
'
C
'
=
a
3
,
sin
A
'
B
'
C
'
^
=
A
'
C
'
B
'
C
'
=
2
3
Mặt khác
B
'
C
'
=
a
3
,
sin
A
'
B
'
C
'
^
=
A
'
C
'
B
'
C
'
=
2
3
Suy ra H K = H B ' sin B ' ^ = a 2 2 3 ; A H = H K tan 60 ° = a 2 2
Do C ' H = A ' H 2 + A ' C ' 2 = 3 a 2 ⇒ r H B ' C ' = H C ' 2 sin H B ' C ' ^ = 3 a 6 8
Áp dụng công thức tính nhanh R = r 2 + A H 2 4 = a 62 8 .

Chọn D

Gọi N, K là trung điểm của BB', A'B'
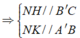
![]()
Ta tính được
![]()
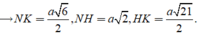
Áp dụng định lí hàm cosin ta suy ra

Cách 2. Chọn hệ trục tọa độ Oxyz với
![]()
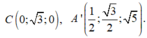
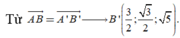

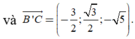
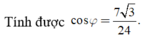

Đáp án: C
Gọi H là trung điểm BC ⇒ A ' H ⊥ ( A B C )
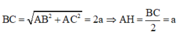
![]()
S ∆ A B C = 1 2 A B . A C = a 2 3 2
Kết luận V = a 3 . a 2 3 2 = 3 a 3 2