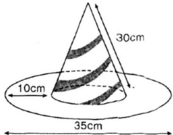
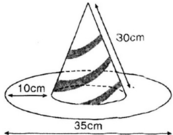
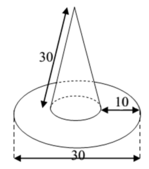
Một cái mũ bằng vải của nhà ảo thuật gia gồm phần dạng hình trụ (có tổng diện tích vải là S 1 ) và phần dạng hình vành khăn (có tổng diện tích vải là S 2 ) với các kích thước như hình vẽ. Tính tổng r + d sao cho biểu thức P = 3 S 2 − S 1 đạt giá trị lớn nhất. (Không kể viền, mép, phần thừa).
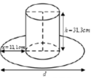
A. 28,6
B. 26,2
C. 30,8
D. 28,2

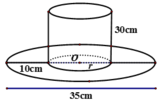



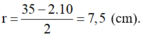
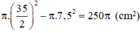
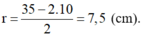
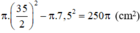
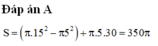
Đáp án D
Diện tích S 1 là S 1 = 2 π r h + π r 2 = 62 , 6 π r + π r 2 ( diện tích toàn phần trừ một đáy)
Diện tích S 2 là S 2 = π 11 , 1 + r 2 − π r 2 = π 123 , 21 + 22 , 2 r ( diện tích hình tròn to trừ hình tròn nhỏ)
Khi đó:
P = 3 S 2 − S 1 = 3 π 22 , 2 r + 123 , 21 − 62 , 6 π r − π r 2 = 369 , 63 π + 4 π r − π r 2
Ta có:
4 r − r 2 = 4 − 2 − r 2 ≤ 4 ⇔ π 4 r − r 2 ≤ 4 π ⇒ P ≤ 373 , 63 π
Dấu “=” xảy ra khi và chỉ khi:
r = 2 ⇒ d = 2 x + r = 2 11 , 1 + 2 = 26 , 2 ⇒ r + d = 28 , 2