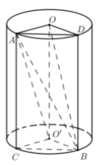
Cho hình trụ có bán kính đáy là R, độ dài đường cao là b. Đường kính MN của đáy dưới vuông góc với đường kính PQ đáy trên. Thể tích của khối tứ diện MNPQ bằng
A. 2 3 R 2 h
B. 1 6 R 2 h
C. 1 3 R 2 h
D. 2 R 2 h
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
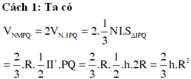
Cách 2:
Gọi I và I’ là tâm của 2 đáy của hình trụ như hình vẽ.
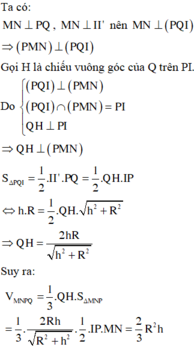

Phương pháp:
+ Gọi C là hình chiếu của A lên mặt đáy chứa đường tròn O ' ; R và D là hình chiếu của B lên mặt đáy chứa đường tròn (O;R).
+) Tính thể tích lăng trụ đứng O A D . O ' C B , từ đó suy ra thể tích tứ diện OO'AB và đánh giá.
Cách giải:

Chọn: D

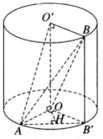
Vì trục OO’ vuông góc với các đáy nên OO′ ⊥ OA; OO′ ⊥ O′B. Vậy các tam giác AOO’ và BO’O vuông tại O và O’.
Theo giả thiết ta có AO ⊥ O′B mà AO ⊥ OO′ ⇒ AO ⊥ (OO′B). Do đó, AO ⊥ OB nên tam giác AOB vuông tại O. Tương tự, ta chứng minh được tam giác AO’B vuông tại O’. Thể tích hình chóp OABO’ là:
![]()
Hay
![]()


Do đó bán kính đường tròn \(\left(S\right)\cap\left(S'\right)\) bằng \(\dfrac{10\sqrt{41}}{41}a\)

Chọn đáp án C.
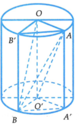
Kẻ các đường sinh AA', BB' của hình trụ (T).
Khi đó
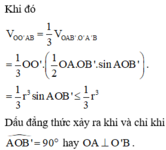
Như vậy, khối tứ diện có thể tích lớn nhất bằng
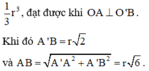
Đáp án A