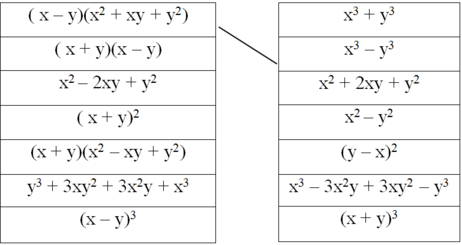
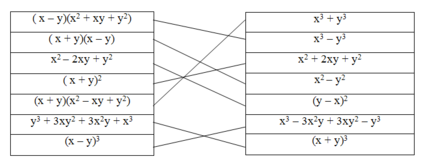
Dùng bút chì nối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức (theo mẫu):
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


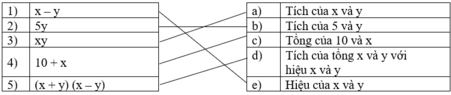
Ý 1) đã cho là x – y được đọc là hiệu của x và y. Đem so sánh với các ý cần nối kết thì ta chọn ý e) vì chúng có cùng ý nghĩa.
Ý 2): Biểu thức 5y được đọc là Tích của 5 và y. Nối 2) với b)
Ý 3): Biểu thức xy được đọc là Tích của x và y. Nối 3) với a)
Ý 4): Biểu thức x + y được đọc là Tổng của 10 và x. Nối 4) với c)
Ý 5): Biểu thức (x + y)(x - y) được đọc là Tích của tổng x và y với hiệu của x và y. Nối 5) với d)

c) \(\left(x^2-y^2\right)^2=x^4-2x^2y^2+y^4\)
c) \(\left(x^2+3^2\right)^2=x^4+18x+81\)
c) \(\left(2x^2+1\right)^2=4x^4+4x^2+1\)
c) \(\left(3x-y^2\right)^2=9x^2-6xy^2+y^4\)
c) \(\left(x+2y^2\right)^2=x^2+4xy^2+4y^4\)
c) \(\left(3x\right)^2-y^2=\left(3x-y\right)\left(3x+y\right)\)
c) \(\left(2x+3y^2\right)^2=4x^2+12xy^2+9y^4\)
c) \(\left(4x-2y^2\right)^2=16x^2-16xy^2+4y^4\)
c) \(\left(4x^2-2y\right)^2=16x^4-16x^2y+4y^2\)
c) \(\left(\dfrac{1}{x}-5\right)\left(\dfrac{1}{x}+5\right)=\dfrac{1}{x^2}-25\)
c) \(\left(x-\dfrac{3}{2}\right)\left(x+\dfrac{3}{2}\right)=x^2-\dfrac{9}{4}\)
c) \(\left(\dfrac{x}{3}-\dfrac{y}{4}\right)\left(\dfrac{x}{3}+\dfrac{y}{4}\right)=\dfrac{x^2}{9}-\dfrac{y^2}{16}\)
c) \(\left(\dfrac{x}{y}-\dfrac{2}{3}\right)\left(\dfrac{x}{y}+\dfrac{2}{3}\right)=\dfrac{x^2}{y^2}-\dfrac{4}{9}\)
c) \(\left(\dfrac{x}{2}+\dfrac{y}{3}\right)\left(\dfrac{y}{3}-\dfrac{x}{2}\right)=\dfrac{y^2}{9}-\dfrac{x^2}{4}\)
c) \(\left(2x-\dfrac{2}{3}\right)\left(\dfrac{2}{3}+2x\right)=4x^2-\dfrac{4}{9}\)
c) \(\left(2x+\dfrac{3}{5}\right)\left(\dfrac{3}{5}-2x\right)=\dfrac{9}{25}-4x^2\)
c) \(\left(\dfrac{1}{2}x-\dfrac{4}{3}\right)\left(\dfrac{4}{4}+\dfrac{1}{2}x\right)=\dfrac{1}{4}x^2-\dfrac{16}{9}\)
c) \(\left(\dfrac{2}{3}x^2-\dfrac{y}{2}\right)\left(\dfrac{2}{3}x^2+\dfrac{y}{2}\right)=\dfrac{4}{9}x^4-\dfrac{y^2}{4}\)

Nối các điểm giao nhau giữa các gợn lồi hoặc của các gợn lõm của hai nguồn sóng với mỗi nguồn, đo khoảng cách \(x_1,x_2\). Tính \(\dfrac{x_1-x_2}{\lambda}\) với \(\lambda\) được xác định trong câu hỏi trước. Nếu thương số nhận được là một số nguyên thì kết quả đúng với công thức.

`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`
`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`
`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`
`=a-b`
`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`
`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`
`=(a^[1/3])^3-(b^[2/3])^3`
`=a-b^2`

x^2 + y^2 = (x + y +\(\sqrt{2xy}\))(x + y - \(\sqrt{2xy}\))