Cho hình lập phương ABCD.A′B′C′D′. Gọi O là tâm của hình vuông ABCD. Côsin của góc giữa hai mặt phẳng (OA′B′) và (OC′D′) bằng
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M, N lần lượt là trung điểm các cạnh A′B′,C′D′ ta có ((OA′B′), (OC′D′)) = (OM,ON).
Ta có
MN=a, 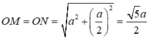
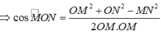
= 3 5
Chọn đáp án D.

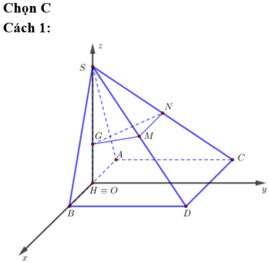
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó
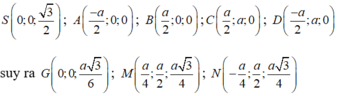
Ta có mặt phẳng (ABCD) có vectơ pháp tuyến là ![]() , mặt phẳng (GMN) có vectơ pháp tuyến là
, mặt phẳng (GMN) có vectơ pháp tuyến là 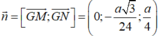
Gọi (α) là góc giữa hai mặt phẳng (GMN) và (ABCD), ta có
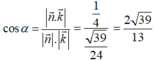
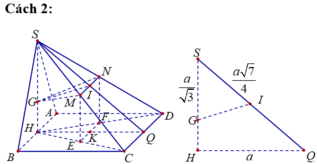
Gọi E, F lần lượt là hình chiếu của M và N lên (ABCD). Suy ra E, F lần lượt là trung điểm của HC, HD.
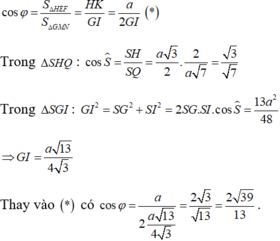
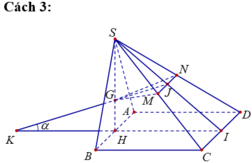
Gọi H, I lần lượt là trung điểm của AB, CD.
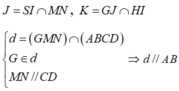
Mà d ⊥ (SIH) nên góc giữa góc giữa hai mặt phẳng (GMN) và (ABCD) là ![]()
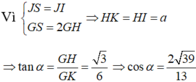

Đáp án A
Chọn gốc tọa độ tại D, các tia Ox, Oy, Oz trùng với các tia DC,DA,DD'.
![]()
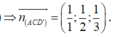
Và B(1;2;0)
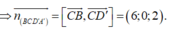
Do đó
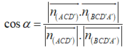
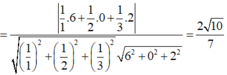
ĐÁP ÁN: D