Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = a . Cạnh bên SA vuông góc với mặt phẳng đáy. Trong các tam giác sau, tam giác nào không phải là tam giác vuông?
A. Δ S A B
B. Δ S B D
C. Δ S C D
D. Δ S B C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

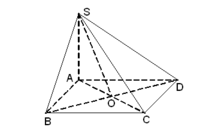
● SA ⊥ (ABCD) ⇒ SA ⊥ AB, SA ⊥ AD.
⇒ Các tam giác SAB, SAD vuông tại A.
● BC ⊥ SA, BC ⊥ AB.
⇒ BC ⊥ SB ⇒ ΔSBC vuông tại B.
● CD ⊥ SA, CD ⊥ AD.
⇒ CD ⊥ SD ⇒ ΔSCD vuông tại D.

Đáp án là A
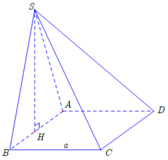
Gọi H là trung điểm A B .
Ta có S A B ⊥ A B C D S A B ∩ A B C D = A B S H ⊂ S A B ; S H ⊥ A B ⇒ S H ⊥ A B C D .
Khi đó: V S . A B C D = 1 3 S H . S A B C D = 1 3 . a 3 2 . a 2 = a 3 3 6 .
Đáp án B
Vì S A ⊥ A B C D ⊃ A B ⇒ S A ⊥ A B
⇒ Δ S A B vuông tại A
Vì S A ⊥ C D ⊥ A D
⇒ C D ⊥ S A D ⇒ C D ⊥ S D
⇒ Δ S C D vuông tại D
Vì S A ⊥ B C ⊥ A B
⇒ B C ⊥ S A B ⇒ B C ⊥ S B
⇒ Δ S B C vuông tại B
Còn Δ S B D vẫn chưa chắc chắn được