Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 2 2 + y − 3 2 + z − 5 2 = 9 và tam giác ABC với A 5 ; 0 ; 0 , B 0 ; 3 ; 0 , C 4 ; 5 ; 0 . Tìm tọa độ điểm M thuộc cầu (S) sao cho khối tứ diên MABC có thể tích lớn nhất.
A. M 0 ; 0 ; 3
B. M 2 ; 3 ; 2
C. M 2 ; 3 ; 8
D. M 0 ; 0 ; − 3

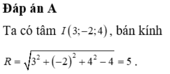



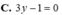

Đáp án C
Mặt cầu (S) có tâm I 2 ; 3 ; 5 ,
Dễ thấy các điểm A, B, C nằm ngoài (S)
Ta có z A = z B = z C = 0 ⇒ A B C : z = 0
V M A B C = S A B C d M ; A B C 3 ≤ S A B C d I ; A B C + R 3
Dấu “=” xảy ra khi M là giao điểm của mặt cầu (S) và đường thẳng ∆ qua tâm I vuông góc (ABC) và xa mặt phẳng(ABC) hơn ⇒ M 2 ; 3 ; 8