Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi I là điểm thuộc AB sao cho A I = a 3 Tính khoảng cách từ điểm C đến (B'DI)
A. 2 a 3
B. a 14
C. a 3
D. 3 a 14
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
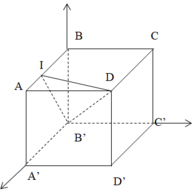
Chọn hệ trục tọa độ như hình vẽ
B ' ( 0 ; 0 ; 0 ) , D ( a ; a ; a ) , I ( 2 a 3 ; 0 ; a ) , C ( 0 ; a ; a ) B ' D → ( a ; a ; a ) , B ' I → ( 2 a 3 ; 0 ; a ) ⇒ n → = [ B ' D → , B ' I → ] = ( a 2 ; − a 2 3 ; − 2 3 a 2 ) ⇒ ( B ' I D ) : 3 x − y − 2 z = 0 ⇒ d ( C , ( B ' I D ) ) = 3 a 14

Chọn C
Ta có AC'=6 nên AB = 2 3 .
Mặt cầu (S) có tâm I(2;4;-1) trùng với tâm hình lập phương ABCD.A'B'C'D' và có bán kính R =1 < A B 2 nên mặt cầu (S) nằm trong hình lập phương ABCD.A'B'C'D'.
Với mọi điểm M nằm trong hình lập phương ABCD.A'B'C'D', tổng các khoảng cách từ điểm M đến 6 mặt của hình lập phương ABCD.A'B'C'D' bằng 3AB = 6 3 .
Vậy từ một điểm M bất kỳ thuộc mặt cầu (S), tổng các khoảng cách từ điểm M đến 6 mặt của hình lập phương ABCD.A'B'C'D' bằng 6 3 .
Đáp án D
Chọn hệ trục tọa độ như hình vẽ
B ' 0 ; 0 ; 0 , D a ; a ; a , I 2 a 3 ; 0 ; a , C 0 ; a ; a B ' D → a ; a ; a , B ' I → 2 a 3 ; 0 ; a ⇒ n → = B ' D → ; B ' I → = a 2 ; - a 2 3 ; - 2 3 a 2 ⇒ B ' I D : 3 x - y - 2 z = 0 ⇒ d C ; B ' I D = 3 a 14