Cho hàm số
y
=
3
−
x
x
+
1
có đồ thị (H). Một phép dời hình biến (H) thành (H') có tiệm cận ngang y = 2 và tiệm cận đứng x = 2. Lấy đối xứng (H’) qua gốc toạ độ được hình (H''). Tìm phương trình của (H'') A.
y
=
6
−
2
x
x
+
2
B.
y
=
2
x
−
6
x
+
2
C.
y
=
...
Đọc tiếp
Cho hàm số y = 3 − x x + 1 có đồ thị (H). Một phép dời hình biến (H) thành (H') có tiệm cận ngang y = 2 và tiệm cận đứng x = 2. Lấy đối xứng (H’) qua gốc toạ độ được hình (H''). Tìm phương trình của (H'')
A. y = 6 − 2 x x + 2
B. y = 2 x − 6 x + 2
C. y = − 2 x x + 2
D. y = 2 x x + 2
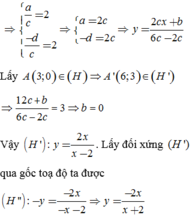
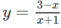có đồ thị (H)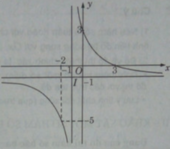
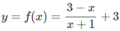
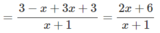
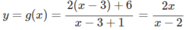
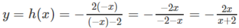
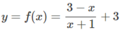
Đáp án C
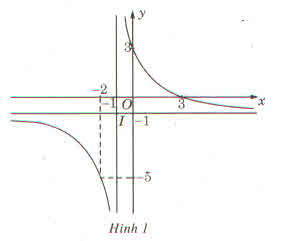
Xét đồ thị hàm số y = 3 − x x + 1 đường tiệm cận ngang y = − 1 và đường tiệm cận đứng x = − 1 . Gọi I − 1 ; − 1 là giao điểm của hai đường tiệm cận của đồ thị (H). Gọi I ' 2 ; 2 là giao điểm của hai đường tiệm cận của đồ thị
Phép dời hình đồ thị (H )thành là phép tịnh tiến theo vecto v → = I I ' → = 3 ; 3
Giả sử đồ thị (H') có phương trình y = a x + b c x + d ; a d − b c ≠ 0
⇒ a c = 2 − d c = 2 ⇒ a = 2 c − d = 2 c ⇒ y = 2 c x + b 6 c − 2 c
Lấy
A 3 ; 0 ∈ H ⇒ A ' 6 ; 3 ∈ H ' ⇒ 12 c + b 6 c − 2 c = 3 ⇒ b = 0
Vậy H ' : y = 2 x x − 2 . Lấy đối xứng (H') qua gốc toạ độ ta được H ' ' : − y = − 2 x − x − 2 ⇒ y = − 2 x x + 2