Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Ta có SC là đường kính của mặt cầu ngoại tiếp hình chóp S.ABCD vì các góc ở đỉnh A, B, D đều nhìn SC dưới góc 90 độ
Đáp án A
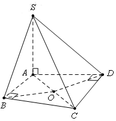
Tam giác ADC vuông tại D ⇒ S Δ A D C = 1 2 . A D . C D = a 2 3 2
⇒ C D = a 3 ⇒ A C = A D 2 + C D 2 = a 2 + a 3 2 = 2 a .
Vì tứ giác ABCD có A B C ⏜ = A D C ⏜ = 90 ∘ ⇒ A B C D là tứ giác nội tiếp đường tròn tâm O với O là trung điểm của AC ⇒ R A B C D = A C 2 = a .
Và S A ⊥ A B C D ⇒ S C ; A B C D ⏜ = S C ; A C ⏜ = S C A ⏜ = 60 ∘
Tam giác SAC vuông tại A ⇒ tan S C A ⏜ = S A A C ⇒ S A = 2 a 3 .
Suy ra bán kính mặt cầu cần tính là:
R = R 2 A B C D + S A 2 4 = 2 a ⇒ S m c = 16 π a 2 .
Đáp án A.
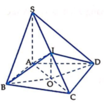
1. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có
C B ⊥ A B , C B ⊥ S A , A B ∩ S A = A ⇒ C B ⊥ S A B ⇒ C B ⊥ S B ⇒ Δ S B C
vuông tại B.
Lại có
C D ⊥ A D , C D ⊥ S A , A D ∩ S A = A ⇒ C D ⊥ S A D ⇒ C D ⊥ S D
⇒ Δ S D C vuông tại D.
Mặt khác S A ⊥ A B C D ⇒ S A ⊥ A C ⇒ Δ S A C vuông tại A.
Gọi I là trung điểm của SC. Các tam giác: Δ S A C , Δ S B C , Δ S D C lần lượt vuông tại các đỉnh A, B và D nên I S = I A = I B = I C = I D = 1 2 S C . Vậy mặt cầu ngoại tiếp hình chóp S.ABCD có tâm I, bán kính R = 1 2 S C
2. Tính diện tích mặt cầu
Ta có S C , A B C D ^ = S C , A C ^ = S C A ^ = 60 °
Do Δ A D C vuông tại A nên S ?A C = 1 2 A D . C D ⇔ A D = 2 S Δ A D C C D = a 2 3 a = a 3
⇒ A C = A D 2 + C D 2 = a 3 2 + a 2 = 2 a
Mà A C = S C . cos S C A ^ ⇒ S C = 2 a cos 60 ° = 4 a
Vậy bán kính của mặt cầu ngoại tiếp hình chóp S.ABCD là R = S C 2 = 4 a 2 = 2 a và diện tích mặt cầu là S = 4 π R 2 = 4 π . 2 a 2 = 16 π a 2 (đvdt).
Đáp án A
Đặt a> 0 cạnh hình vuông là Dễ thấy
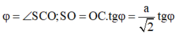
Gọi O là tâm của đáy. Vẽ AH ⊥ SC tại, H, AH cắt SO tại I thì A I O ^ = φ
Qua I vẽ đường thẳng song song DB cắt SD, SB theo thứ tự tại K, L. Thiết diện chính là tứ giác
ALHK và tứ giác này có hai đường chéo AH ⊥ KL Suy ra
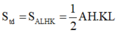
Ta có:
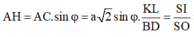
Theo giả thiết
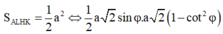
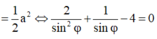
Giải được
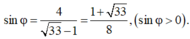
Suy ra φ = a r c sin 33 + 1 8
Đáp án A
Ta có SC là đường kính của mặt cầu ngoại tiếp hình chóp S.ABCD vì các góc ở đỉnh A, B, D đều nhìn SC dưới góc 90 độ S B C ^ = S D C ^ = S A C ^ = 90 0 . Do đó bán kính của mặt cầu là R = 1 2 SC.
Tam giác ADC vuông tại D có