Trong không gian Oxy cho điểm , véc-tơ và đường thẳng d: . Viết phương trình đường thẳng đi qua A, vuông góc ới giá của và cắt d.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Hình chiếu vuông góc của điểm M ( x 0 ; y 0 ; z 0 ) trên mặt phẳng (Oxy) là điểm M ' ( x 0 ; y 0 ; z 0 )
Cách giải:
Hình chiếu vuông góc của điểm A(1;2;3) trên mặt phẳng (Oxy) là điểm N(1;2;0)

Đáp án A
Phương pháp:
Hình chiếu vuông góc của điểm M(x0;y0;z0) trên mặt phẳng (Oxy) là điểm M’(x0;y0;z0)
Cách giải:
Hình chiếu vuông góc của điểm A(1;2;3) trên mặt phẳng (Oxy) là điểm N(1;2;0)

Đáp án C
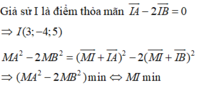
Suy ra M là hình chiếu vuông góc của I lên (Oxy) => I(3;-4;0)

Đáp án A.
Cách giải:
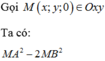
![]()
Thử lần lượt 4 đáp án thì ta thấy với M(3;-4;0)
thì M A 2 - 2 M B 2 = 3 là lớn nhất.





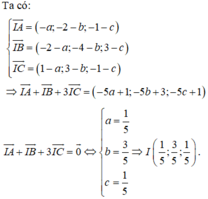
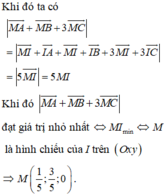

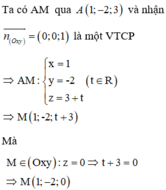
Đáp án A
Goi (P) là mặt phẳng đi qua A vuông vởi với giá của u →
⇒ P : 6 x + 1 − 2 y − 2 − 3 z + 3 = 0 ⇔ P : 6 x − 2 y − 3 z = − 1
Gọi B = P ∩ d ⇒ B 4 + 3 t ; 1 + 2 t ; − 2 − 5 t
B ∈ P ⇒ 6. 4 + 3 t − 2 1 + 2 t − 3 − 2 − 5 t = − 1 ⇔ t = − 1 ⇒ B 1 ; − 1 ; 3
Đường thẳng Δ đi qua A − 1 ; 2 ; − 3 và B 1 ; − 1 ; 3 có vtcp u Δ → = A B → = 2 ; − 3 ; 6
⇒ Δ : x − 1 2 = y + 1 − 3 = z − 3 6