Ống dây dẫn hình trụ có lõi chân không, dài 20 cm, gồm 1000 vòng dây, mỗi vòng dây có diện tích 100 c m 2 . Tính năng lượng từ trường tích luỹ trong ống dây khi cường độ dòng điện chạy qua ống dây đạt tới giá trị 5,0 A.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Độ lớn của suất điện động tự cảm xuất hiện trong ống dây dẫn
![]()

Từ thông qua ống dây dẫn gồm N vòng dây tính bằng Φ = NBS. Vì cảm ứng từ B tăng, nên từ thông Φ tăng theo sao cho : ∆ Φ = NS ∆ B.
Áp dụng công thức của định luật Fa-ra-đây, ta xác định được độ lớn của suất điện động cảm ứng xuất hiện trong ống dây dẫn :
![]()
Từ đó suy ra cường độ dòng điện cảm ứng chạy trong ống dây dẫn :
![]()
Áp dụng định luật Jun - Len-xơ, ta tính được công suất nhiệt toả ra trong ống dây dẫn :
P = R i c 2 = 16. 25 . 10 - 3 2 = 10mW

Vì từ thông qua ống dây đồng có trị số Φ = Li, nên từ thông qua mỗi vòng dây khi dòng điện chạy trong ống dây có cường độ i = I = 2,5 A sẽ bằng :
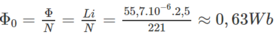
và năng lượng từ trường tích luỹ trong ống dây đồng tính bằng :
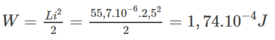

a) Ống dây không có lõi sắt, độ tự cảm của một ống dây:
![]()
b) Ống dây có lõi sắt với độ từ thẩm μ = 400 , độ tự cảm của một ống dây:
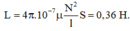

Độ tự cảm của ống dây:
L = 4 π . 10 - 7 . μ . N 2 I S = 4 π . 10 - 7 . 1 . 1000 2 0 , 2 . 10 - 2 = 6 , 283 . 10 - 3 ( H ) .
a) e t c = L . ∆ i ∆ t = 6 , 283 . 10 - 3 . 2 − 0 0 , 01 = 1 , 26 ( V ) .
b) e ' t c = L . ∆ i ' ∆ t
⇒ ∆ i ' I ' - 0 = I ' = | Δ i | . | e ' t c | | e t c | = 2.3 1 , 26 = 4 , 76 ( A ) .

Mai dậy sớm xem bài tui làm nha :>
a/ \(\left|e_C\right|=N\left|\dfrac{\Delta\phi}{\Delta t}\right|=\dfrac{N\left|\Delta B\right|S}{\Delta t}=\dfrac{N\left|\Delta B\right|.\pi d^2}{4\Delta t}=\dfrac{1000.0,01.3,14.\left(10^{-2}\right)^2}{4}=...\left(V\right)\)
b/ \(W=\dfrac{1}{2}CU^2=\dfrac{1}{2}C.e_C^2=\dfrac{1}{2}.10^{-4}.e_C^2=...\left(J\right)\)
\(\Rightarrow Q=C.U=C.e_C=10^{-4}.e_C=...\left(C\right)\)
c/ \(l=N\pi d=1000.3,14.10^{-2}=...\left(m\right)\)
\(\Rightarrow R=\rho.\dfrac{l}{S}=1,75.10^{-8}.\dfrac{1000.3,14.10^{-2}}{0,4.10^{-6}}=...\left(\Omega\right)\)
\(i_C=\dfrac{e_C}{R}=...\left(A\right)\)
\(\Rightarrow P=e_C.i_C=...\left(W\right)\)

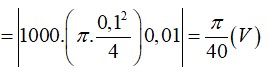
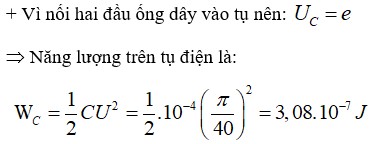




Năng lượng từ trường tích lũy trong ống dây dẫn: