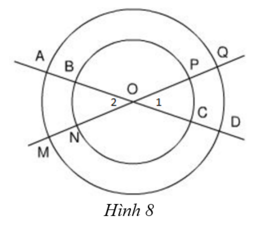
Cho hai đường tròn cùng tâm O với bán kính khác nhau. Hai đường thẳng đi qua O cắt hai đường tròn đó tại các điểm A, B, C, D, M, N, P, Q (h.8).
Hãy nêu tên hai cung lớn bằng nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các cung nhỏ có số đo bằng nhau là:
Trong đường tròn lớn:
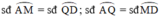
Trong đường tròn nhỏ:
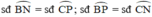

Các cung nhỏ có số đo bằng nhau là:
Trong đường tròn lớn:
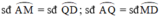
Trong đường tròn nhỏ:
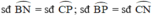


b) Các cung nhỏ có số đo bằng nhau là:
Trong đường tròn lớn:
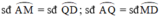
Trong đường tròn nhỏ:
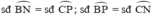
c) Hai cung lớn ![]() có số đo bằng nhau.
có số đo bằng nhau.
* Chú ý : Phân biệt : so sánh hai cung và số đo hai cung.
So sánh hai cung trong trường hợp hai cung trong một đường tròn hoặc trong hai đường tròn có bán kính bằng nhau.
Còn so sánh số đo hai cung : ta luôn so sánh được.
Kiến thức áp dụng
+ Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
+ Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

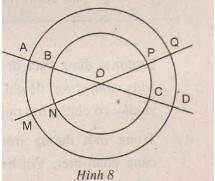
a) các cung nhỏ AM, CP, BN, DQ có cùng số đo
b) cung AM = DQ; cung BN = PC; cung AQ = MD; cung BP = NC.
c) các cung lớn bằng nhau: AQDM = DMAQ; BPCN = PBNC; AMDQ = MAQD; BNCP = NBPC; AQD = AMD = MAQ = MDQ BPC = BNC = NBP = NCP

a. b.
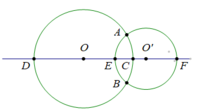
c. - Đường tròn (O’; 1cm) có đường kính là: EF; Các dây cung là: EA, EB, AB, FA, FB
Vì E thuộc (O’; 1cm) nên EO’=1cm; EF=2.EO’=2cm
- Đường tròn (O; 1,5cm) có đường kính là: DC; Các dây cung là: DA, DB, AB, AC, CB
Vì C thuộc (O; 1,5cm) nên CO=1,5cm; DC=2.CO=3cm
d. Vì đường tròn (O’; 1cm) cắt đoạn thẳng OO’ tại E, nên E nằm giữa 2 điểm O và O’.
Ta có: O E + E O ' = O O ' ⇒ O E = 1 c m
Mà EO’=1cm, nên OE=EO’ (=1cm)
Do đó: E là trung điểm của đợn thẳng OO’.
e. Vì đường tròn (O; 1cm) cắt đường thẳng OO’ tại D, đường tròn (O’; 1cm) cắt đường thẳng OO’ tại F, nên 4 điểm D, O, O’, F lần lượt theo thứ tự đó và DO=1,5cm; O’F=1cm.
Ta có: D F = D O + O O ' + O ' F = 1 , 5 + 2 + 1 = 4 , 5 c m .
Vậy DF=4,5cm
Hai cung lớn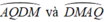 có số đo bằng nhau.
có số đo bằng nhau.
* Chú ý : Phân biệt : so sánh hai cung và số đo hai cung.
So sánh hai cung trong trường hợp hai cung trong một đường tròn hoặc trong hai đường tròn có bán kính bằng nhau.
Còn so sánh số đo hai cung : ta luôn so sánh được.