Một vật khối lượng m ở độ cao ![]() so với mặt đất. Chọn mốc thế năng tại mặt đất, g là gia tốc rơi tự do. Thế năng trọng trường của vật là
so với mặt đất. Chọn mốc thế năng tại mặt đất, g là gia tốc rơi tự do. Thế năng trọng trường của vật là
A. ![]()
B.![]()
C.![]()
D.![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Theo định nghĩa về thế năng:
Khi một vật khối lượng m đặt ở độ cao z so với mặt đất chọn làm mốc thế năng (trong trọng trường của Trái Đất) thì thế năng trọng trường của vật được định nghĩa bằng công thức:
Wt =mgz

`a)W_[t(60m)] = mgz_[60m] = 2 . 10 . 60 = 1200 (J)`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`b)W=W_[đ(max)] = W_[t(max)]`
`<=>1/2mv_[cđ]^2=mgz_[max]`
`<=>1/2 .2.v_[cđ]^2=2.10.80`
`<=>v_[cđ] = 40(m//s)`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`c)W=W_t+W_đ`
Mà `W_đ=3W_t`
`=>W=4W_t`
Hay `W = W_[t(max)]=mgz_[max]=2.10.80=1600(J)`
`=>1600=4W_t`
`=>400=mgz_[(W_đ = 3W_t)]`
`=>400=2.10.z_[(W_đ = 3W_t)]`
`=>z_[(W_đ=3W_t)]=20 (m)`

Chọn gốc tính thế năng ( Z0 = 0) tại mặt đất.
Vận tốc của vật sau khi rơi được quãng đường
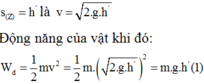
Thế năng của vật tương ứng với vị trí đó bằng:
![]()
IXét tổng quát tại vị trí động năng bằng n thế năng thì
![]()
Giá trị đại số của tọa độ Z của vật so với mốc bằng:
![]()
Thế năng của vật ở vị trí động năng bằng ba thế năng là
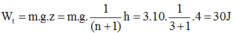

Bài 1:
m = 500g =0,5kg
h =100m
g =10m/s2
Wt =0
a) Wđ =?
b) z =? khiWđ =3Wt
c) Wđ =? z' =50m.
GIẢI :
a) vận tốc lúc chạm đất của vật :
\(v=\sqrt{2gh}=\sqrt{2.10.100}=20\sqrt{5}\left(m/s\right)\)
Động năng của vật khi chạm đất :
\(W_đ=\frac{1}{2}mv^2=\frac{1}{2}.0,5.\left(20\sqrt{5}\right)^2=500\left(J\right)\)
b) Wđ =3Wt
\(W=mgz+\frac{1}{2}mv^2=0,5.10.100+\frac{1}{2}.0,5.\left(20\sqrt{5}\right)^2=1000\left(J\right)\)
=> \(W=W_đ+W_t=3W_t+W_t=4W_t\)
<=> \(1000=4.0,5.10.z\)
=> z = 50(m)
c) h= 50(m) => \(v=\sqrt{2gh}=10\sqrt{10}\left(m/s\right)\)
=> \(W_đ=\frac{1}{2}.0,5.\left(10\sqrt{10}\right)^2=250\left(J\right)\)

a, W= mgh=90J
b, Wt = 1/3Wđ
=> 4/3.1/2.mV2 = 90
=> V \(\approx\) 26
Đáp án A