Cho hình lập phương có cạnh bằng 1. Diện tích của mặt cầu ngoại tiếp hình lập phương đó bằng
A. 3 π
B. 12 π
C. π
D. 6 π
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 6 2019
Đúng(0)
Những câu hỏi liên quan
CM
23 tháng 10 2019
Chọn A.
Gọi 2a là cạnh của hình lập phương thì hình cầu nội tiếp hình lập phương đó có bán kính r = a.
Suy ra:
CM
20 tháng 2 2018
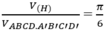
Chọn D.
Gọi 2a là cạnh của hình lập phương ta có hình nón tròn xoay nội tiếp hình lập phương đó có bán kính đáy r = a và chiều cao h = 2a
Suy ra:
CM
12 tháng 8 2019
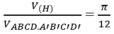
Chọn B
Gọi a là cạnh của hình lập phương ta có hình trụ tròn xoay ngoại tiếp hình lập phương đó có bán kính đáy r = (a 2 )/2 và chiều cao h = a.
Suy ra:
CM
11 tháng 5 2018
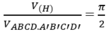
Chọn A.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật, nên mặt cầu (S) có bán kính
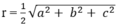
Do đó diện tích mặt cầu (S) là: S = 4 πr 2 = π( a 2 + b 2 + c 2 )
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 8 2021
Gọi O là tâm đáy \(\Rightarrow AO=\dfrac{a\sqrt{3}}{3}\)
\(SA=\dfrac{AO}{cos60^0}=\dfrac{2a\sqrt{3}}{3}\)
\(SO=\sqrt{SA^2-AO^2}=a\)
\(\Rightarrow R=\dfrac{SA^2}{2SO}=\dfrac{2a}{3}\)
\(V=\dfrac{4}{3}\pi R^3=\dfrac{32\pi a^3}{81}\)
\(\Rightarrow\dfrac{V}{\pi a^3}=\dfrac{32}{81}\)