Cho hai điểm A và B.
a) Hãy vẽ một đường tròn đi qua hai điểm đó.
b) Có bao nhiêu đường tròn như vậy ? Tâm của chúng nằm trên đường nào ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 2 2018
Có vô số đường tròn đi qua hai điểm. Tâm của chúng nằm trên đường trung trực của đoạn thẳng đó
CM
19 tháng 1 2018
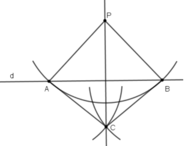
a) Ta có: PA = PB (A; B nằm trên cung tròn tâm P) nên P nằm trên đường trung trực của AB.
CA = CB (C nằm trên 2 cung tròn tâm A, B bán kính bằng nhau) nên C nằm trên đường trung trực của AB.
Vậy CP là đường trung trực của AB, suy ra PC ⊥ d.
QUẢNG CÁOb) Một cách vẽ khác
- Lấy hai điểm A, B bất kì trên d.
- Vẽ cung tròn tâm A bán kính AP, cung tròn tâm B bán kính BP. Hai cung tròn cắt nhau tại C (C khác P).
- Vẽ đường thẳng PC. Khi đó PC là đường đi qua P và vuông góc với d.
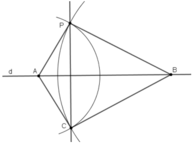
Chứng minh :
- Theo định lí 2 :
PA = CA ( P,C cùng thuộc cung tròn tâm A bán kính PA)
⇒ A thuộc đường trung trực của PC.
PB = CB (P, C cùng thuộc cung tròn tâm B bán kính PB)
⇒ B thuộc đường trung trực của PC.
⇒ AB là đường trung trực của PC
⇒ PC ⏊ AB hay PC ⏊ d.
CM
16 tháng 4 2019
a) HS tự vẽ hình.
b) Hai đường tròn trên có đi qua O và I. Chúng có cắt nhau.
CM
29 tháng 5 2018
a) HS tự vẽ hình.
b) Hai đường tròn trên có đi qua O và I. Chúng có cắt nhau.
31 tháng 12 2023
a: Xét tứ giác ABCO có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABCO là tứ giác nội tiếp đường tròn đường kính OA
=>A,B,C,O cùng thuộc đường tròn đường kính OA
tâm là trung điểm của OA
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại M và M là trung điểm của BC
Xét ΔOCA vuông tại C có CM là đường cao
nên \(OM\cdot OA=OC^2\)
mà OC=OE(=R)
nên \(OE^2=OM\cdot OA\)
c: Ta có: ΔOEF cân tại O
mà OG là đường trung tuyến
nên OG\(\perp\)EF
Xét ΔOGA vuông tại G và ΔOMH vuông tại M có
\(\widehat{GOA}\) chung
Do đó: ΔOGA đồng dạng với ΔOMH
=>\(\dfrac{OG}{OM}=\dfrac{OA}{OH}\)
=>\(OG\cdot OH=OA\cdot OM=OE^2\)
=>\(\dfrac{OG}{OE}=\dfrac{OE}{OH}\)
Xét ΔOGE và ΔOEH có
\(\dfrac{OG}{OE}=\dfrac{OE}{OH}\)
\(\widehat{GOE}\) chung
Do đó: ΔOGE đồng dạng với ΔOEH
=>\(\widehat{OGE}=\widehat{OEH}\)
=>\(\widehat{OEH}=90^0\)
=>HE là tiếp tuyến của (O)
CM
6 tháng 5 2017
a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O1 vì OA = O 1 A = 3 cm.
CM
22 tháng 4 2019
a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O 1 vì O A = O 1 A = 3 c m .
CM
1 tháng 8 2019
- Vì A và B là hai điểm nằm trên đường tròn tâm O nên OA = OB.
- Suy ra O thuộc đường trung trực của đoạn AB.
Vì tâm O nằm trên đường thẳng d nên O là giao điểm của đường trung trực của AB và đường thẳng d.
- Dựng đường thẳng m là đường trung trực của AB cắt d tại O.
- Vẽ đường tròn tâm O bán kính OA (hoặc OB).
* Lưu ý:
- Nếu m // d thì không dựng được tâm O
- Nếu m trùng với d thì có vô số điểm chung O do đó có vô số đường tròn thỏa mãn bài toán.
a)
b) Có vô số đường tròn đi qua hai điểm. Tâm của chúng nằm trên đường trung trực của đoạn thẳng đó