Cho mạch điện như hìh vẽ. Biết điện trở giữa hai nút liên tục là r.
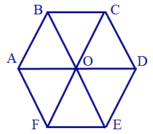
Tính điện trở của đoạn mạch khi dòng điện:
a) Vào A ra D.
b) Vào A ra E.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

nếu mắc nối tiếp:Rtđ=R1+R2+R3+R4+R5...Rn
nếu mắc //:\(\frac{1}{Rtd}\)=\(\frac{1}{R1}\)+\(\frac{1}{R2}\)+.....\(\frac{1}{Rn}\)

a. \(R=R1+\left(\dfrac{R2.R3}{R2+R3}\right)=60+\left(\dfrac{60.120}{60+120}\right)=100\left(\Omega\right)\)
b. \(I=I1=I23=U:R=120:100=1,2A\left(R1ntR23\right)\)
\(U1=I1.R1=1,2.60=72V\)
\(U2=U3=U23=U-U1=120-72=48\left(V\right)\)(R1//R2)
\(\left[{}\begin{matrix}I2=U2:R2=48:60=0,8A\\I3=U3:R3=48:120=0,4A\end{matrix}\right.\)

Chọn D. Điện trở R tỉ lệ thuận với hiệu điện thế U và tỉ lệ nghịch với cường độ dòng điện I chạy qua đoạn mạch
a) Vào A ra D.
- Các đoạn mạch AB và AF; BC và FE; CD và ED đối xứng qua trục đối xứng AD.
- Các đoạn mạch AB và CD; BO và OC; AF và ED; FO và OE đối xứng qua trục đối xứng xy.
Do 2 sự đối xứng nói trên nên dòng điện qua các đoạn mạch đối xứng sẽ bằng nhau và có chiều như hình vẽ.
Vì vậy ta có thể nhả nút O mà vẫn không làm thay đổi dòng điện qua các đoạn mạch.
Ta có: R A B C O D = r + r . 2 r r + 2 r + r = 2 r + 2 r 3 = 8 r 3 ;
R A O D = 2 r ; 1 R A D = 2 . 3 8 r + 1 2 r = 10 8 r ⇒ r A D = 0 , 8 r
b) Vào A ra E.
- Các đoạn mạch AB và DE; BC và CD; BO và OD; AO và OE; AF và FE đối xứng qua trục đối xứng FC, nên các dòng điện chạy qua các đoạn mạch này bằng nhau.
- Nếu xét tại nút C (hoặc F) ta thấy dòng điện qua các đoạn OC và OF bằng 0.
Vì vậy ta có thể nhả nút O mà không làm không làm thay đổi dòng điện trong mạch.
Ta có:
R A B D E = r + 2 r . 2 r 2 r + 2 r + r = 3 r ; 1 r A E = 1 2 r + 1 2 r + 1 3 r = 3 + 3 + 2 6 r = 4 3 r ⇒ r A E = 3 r 4 = 0 , 75 r .