Con lắc lò xo gồm vật nặng khối luợng m = 100 g và lò xo có độ cứng k = 100 N/m chịu tác dụng của ngoại lực biến thiên theo thời gian có phuơng trình 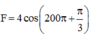 N. Bỏ qua mọi lực cản. Lấy
π
2
= 10. Tần số góc của con lắc là.
N. Bỏ qua mọi lực cản. Lấy
π
2
= 10. Tần số góc của con lắc là.
A. 10 π
B.100 π
C. 20 π
D.200 π


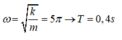
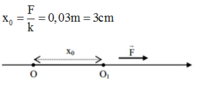
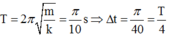
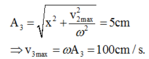
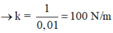


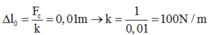
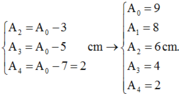
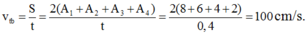
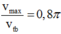
Đáp án D
Tần số góc của con lắc bằng tần số của ngoại lực biến thiến theo thời gian