Cho hình chóp tam giác đều S.ABC đỉnh S. Có độ dài cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I là trung điểm của cạnh BC. Tính thể tích V của khối chóp S.ABI
A. V = a 3 11 12
B. V = a 3 11 24
C. V = a 3 11 8
D. V = a 3 11 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi O là hình chiếu của S lên A B C ; S O = S B 2 − B O 2 = 4 a 2 − a 2 3 = a 33 3
V = 1 3 S Δ A B I . S O = 1 3 . a 2 3 8 . a 33 3 = a 3 11 24

Đáp án B
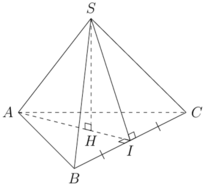
Gọi H là hình chiếu vuông góc của S trên mặt phẳng (ABC), khi đó:
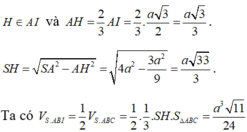

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\)
\(\Rightarrow\widehat{SAO}=60^0\Rightarrow AO=SA.cos60^0=a\)
\(R=a;l=2a\Rightarrow h=SO=\sqrt{\left(2a\right)^2-a^2}=a\sqrt{3}\)
\(V=\dfrac{1}{3}\pi R^2h=\dfrac{\sqrt{3}}{3}\pi a^3\)

a:ΔSBC cân tại S có SM là trung tuyến
nên SM vuông góc BC
BC=6cm
=>BM=CM=3cm
SM=căn 5^2-3^2=4cm
Sxq=5*3/2*4=5*3*2=30cm2
Stp=30+5^2*căn 3/2=(60+25căn 3)/2cm2
b: BC vuông góc SM
BC vuông góc AM
=>BC vuông góc (SAM)

Đáp án D
Gọi H là trung điểm của BC, khi đó từ giả thiết ta có A'H ⊥ (ABC). Ta có:
A'H = a 3 => V A . BCC ' B ' = V ABC . A ' B ' C ' - V A ' . ABC
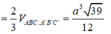

Đáp án D
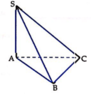
Do Δ A B C đều có cạnh bằng 2a nên
S Δ A B C = 2 a 2 . 3 4 = a 2 3 (đvdt).
Thể tích khối chóp S.ABC là: V S . A B C = 1 3 S A . S Δ A B C = 1 3 . a 3 . a 2 3 = a 3