Cho ba số tạo thành một cấp số nhân mà tổng của chúng bằng 93. Ta có thể sắp xếp chúng (theo thứ tự của cấp số nhân kế trên) như là số hạng thứ nhất, thứ hai và thứ bảy của một cấp số cộng. Tìm tích của 3 số đó.
A. 3375
B. 64
C. 2744
D. 1000
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 4 2016
Gọi 3 số đã cho là \(u_1;u_2;u_3\), theo thứ tự là 3 số của một cấp số cộng
Còn cấp số nhân \(\left(v_n\right)\). Theo giả thiết ta có hệ :
\(\Leftrightarrow\begin{cases}v_1+v_2+v_3+v_4=93\left(a\right)\\v_1=u\left(1\right)_1\\u_1+d=v_1q\left(2\right)\\u_1+2d=v_1q^2\left(3\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}v_1\left(1+q+q^2\right)=93\left(a\right)\\d=u_1\left(q-1\right)\left(1V2\right)\left(4\right)\\6d=u_3-u_1=u_1\left(q^2-1\right)\left(2V3\right)\left(5\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}u_1\left(1+q+q^2\right)=93\left(a\right)\\u_1\left(q-1\right)=\frac{1}{6}u_1\left(q^2-1\right)\left(4V5\right)\left(6\right)\\d=u_1\left(q-1\right)\end{cases}\)
Từ (1) và (2) cho ta phương trình (4). Còn từ (2) và (3) cho phương trình (5). Mặt khác ừ (4) và (5) cho phương trình (6)
Do \(u_1\ne0,q\ne1\Rightarrow\left(6\right)\Leftrightarrow1=\frac{1}{6}\left(q+1\right)\Leftrightarrow q=5\)
Theo (a) : \(v_1+5v_1+25v_1=93\Leftrightarrow u_1=3\)
Vậy 3 số cần tìm là : 3,15,75
CM
30 tháng 12 2019
Chọn A
Gọi u1,u2,u3,u4 là 4 số hạng đầu tiên của cấp số nhân, với công bội q. gọi (vn) là cấp số cộng tương ứng với công sai là d. Theo giả thuyết Ta có:
u 1 + u 2 + u 3 = 16 4 9 u 1 = v 1 u 2 = v 4 = v 1 + 3 d u 3 = v 8 = v 1 + 7 d ⇔ u 1 + u 1 q + u 2 q 2 = 16 4 9 1 u 1 q = u 1 + 3 d 2 u 1 q 2 = u 1 + 7 d 3
Khử d từ (2) và (3) ta thu được:
7 u 1 q = 7 u 1 + 21 d 3 u 1 q 2 = 3 u 1 + 21 d
Lấy vế trừ vế ta thu được
7 u 1 q − 3 u 1 q 2 = 4 u 1 ⇔ u 1 . 3 q 2 − 7 q + 4 = 0 ⇔ u 1 = 0 3 q 2 − 7 q + 4 = 0
Do u 1 ≠ 0 ⇒ q = 1 q = 4 3
Theo định nghĩa cấp số nhận thì q ≠ 1 . Do đó q = 4 3
Thay q = 4 3 vào (1) ta được u 1 = 4
CM
2 tháng 1 2017
Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
BT
25 tháng 5 2017
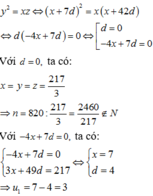
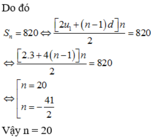
Gọi ba số đó là \(x,y,z\). Do ba số là các số hạng thứ hai, thứ 9 và thứ 44 của một cấp số cộng nên:
\(x;y=x+7d;z=x+42d\). (Với d là công sai của cấp số cộng).
Ta có: \(x+y+z=x+x+7d+x+42d=3x+49d=217\).
Mặt khác x, y, z là các số hạng liên tiếp của một cấp số nhân nên:
\(y^2=xz\)\(\Leftrightarrow\left(x+7d\right)^2=x\left(x+42d\right)\)\(\Leftrightarrow-28xd+49d^2=0\)\(\Leftrightarrow7d\left(-4x+7d\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}d=0\\-4x+7d=0\end{matrix}\right.\).
Với \(d=0\) suy ra \(x=y=z=\dfrac{217}{3}\).
Suy ra: \(n=820:\dfrac{217}{3}=\dfrac{2460}{217}\notin N\).
Với \(4+7d=0\). Ta có hệ:
\(\left\{{}\begin{matrix}4x+7d=0\\3x+49d=217\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=7\\d=4\end{matrix}\right.\).
Vậy \(u_1=7-4=3\).
Có \(S_n=\dfrac{\left[2u_1+\left(n-1\right)d\right]n}{2}=\dfrac{\left[2.3+\left(n-1\right)4\right]n}{2}=820\)
\(\Rightarrow n=20\left(tm\right)\).
Gọi ba số đã cho u1,u2,u7 theo thứ tự là ba số của một cấp số cộng (un) và v1,v2, v3 của cấp số nhân (vn) . Theo giả thiết Ta có hệ:
Giải phương trình (6)
( 6 ) ⇔ u 1 q − 1 = 1 6 u 1 q − 1 q + 1 ⇔ u 1 q − 1 = 0 ( l o a i ) 1 = 1 6 q + 1
Thay vào (*), ta được
u 1 1 + 5 + 5 2 = 93 ⇔ u 1 = 3 = v 1
Suy ra
u 2 = u 1 . q = 3.5 = 15 = v 2 u 3 = u 1 . q 2 = 3.25 = 75 = v 3
Vậy tích ba số v 1 . v 2 . v 3 = 3.15.75 = 3375
Đáp án A