Chứng tỏ rằng trong chuyển động thẳng nhanh dần đều không có vận tốc đầu, quãng đường đi được trong những khoảng thời gian bằng nhau liên tiếp tỉ lệ với các số lẻ liên tiếp 1, 3, 5,….
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án A
+ Ta có công thức tính đường đi: s = 1 2 a t 2 + v 0 t
+ Theo đề t 1 = 4 s ; s 1 = 24 m t 1 + t 2 = 8 s : s 1 + s 2 = 88 m ; 8 a + 4 v 0 = 24 32 a + 8 v 0 = 88 ⇒ v 0 = 1 m / s a = 2 , 5 m / s 2

Ta có công thức tính đường đi v 2 d = v 1 a
Theo đề: t 1 = 4 s : s 1 = 24 m t 1 + t 2 = 8 s : s 1 + s 2 = 88 m ⇒ 8 a + 4 v 0 = 24 32 a + 8 v 0 = 88
Giải hệ phương trình này ta được: v 0 = 1 m / s ; a = 2 , 5 m / s 2

Một vật chuyển động thẳng nhanh dần đều, đi được những đoạn đường s1=35m, s2=120m trong khoảng thời gian liên tiếp bằng nhau là 5 giây, gia tốc và vận tốc ban đầu của vật lần lượt là:
A. 1m/s2; 4,5m/s.
B. 2m/s2; 2m/s.
C. 1,2m/s2; 4m/s.
D. 1m/s2; 1,2m/s.
Bài giải:
Phương trình quãng đường của vật: \(S=v_0t+\dfrac{1}{2}at^2\)
Trong 5s vật đi được: \(S_1=v_0t+\dfrac{1}{2}at^2=35\left(m\right)\)
Trong \(\left(5+5=10s\right)\) vật đi được: \(S_2=v_0t+\dfrac{1}{2}at^2=120\left(m\right)\)
Từ 2 pt trên: \(\Rightarrow\left\{{}\begin{matrix}v_0=2\\a=2\end{matrix}\right.\)
Chọn B.

đáp án của bài này là B
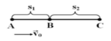
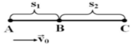
S1= vot + at^2/2=12 <=> S1= vo.4 + 8a= 24
S12= vot + at^2/2= S1 +S2= 88 <=> vo8 + 32a = 88
Giải hệ ta đc a= 2,5 m/s^2
vo=1 m/s
lấy vo/a = 0,4s

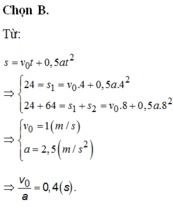
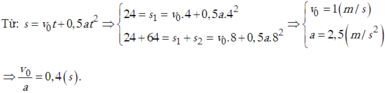
Áp dụng công thức tính đường đi s = 1 2 a t 2 ta được:
s 1 = 1 2 a t 2 ; s 2 = 1 2 a 2 t 2 = 4 2 a t 2 ; s 3 = 1 2 a 3 t 2 = 9 2 a t 2 ... ;
s n − 1 = 1 2 a n − 1 t 2 a t 2 ; s n = 1 2 a n t 2 = n 2 2 a t 2 .
Do đó Δ s 1 = s 1 − 0 = 1 2 a t 2 ; Δ s 2 = s 2 − s 1 = 3 2 a t 2 ; Δ s 3 = s 3 − s 2 = 5 2 a t 2 ... ;
Δ s n = s n − s n − 1 = 1 2 n 2 − n − 1 2 a t 2 = 2 n − 1 2 a t 2 .
Suy ra Δ s 2 Δ s 1 = 3 ; Δ s 3 Δ s 1 = 5 ; ... ; Δ s n Δ s 1 = 2 n − 1 .
Từ đó suy ra Δ s 1 : Δ s 2 : Δ s 3 : ... = 1 : 3 : 5 : ...