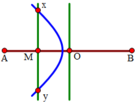
Trên mặt nước có hai nguồn sóng giống nhau A và B, cách nhau khoảng AB = 12 cm đang dao động vuông góc với mặt nước tạo ra sóng có bước sóng λ = 1,6 cm. C và D là hai điểm khác nhau trên mặt nước, cách đều hai nguồn và cách trung điểm O của AB một khoảng 8 cm. Số điểm dao động cùng pha với nguồn ở trên đoạn CD là
A. 5
B. 6
C. 3
D. 10