Tính các tích phân sau bằng phương pháp đổi biến số: I 4 = ∫ - π 4 π 4 1 + tan x cos 2 x d x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

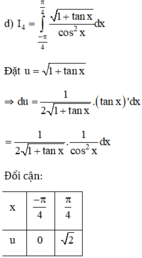
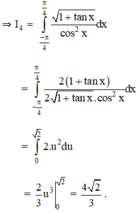

π 2 /4
Hướng dẫn: Đặt x = π − t, ta suy ra:
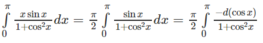
Vậy
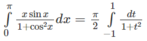
Đặt tiếp t = tanu

\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)

\(cot1,25.tan\left(4\pi+1,25\right)-sin\left(x+\frac{\pi}{2}\right).cos\left(6\pi-x\right)=0\)
\(\Leftrightarrow cot1,25.tan1,25-cosx.cos\left(-x\right)=0\)
\(\Leftrightarrow1-cos^2x=0\)
\(\Leftrightarrow sin^2x=0\Rightarrow sinx=0\Rightarrow tanx=0\)

1.
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2}cos4x=\dfrac{1}{2}+\dfrac{1}{2}cos\left(2x-\dfrac{\pi}{2}\right)\)
\(\Leftrightarrow-cos4x=cos\left(2x-\dfrac{\pi}{2}\right)\)
\(\Leftrightarrow cos\left(4x-\pi\right)=cos\left(2x-\dfrac{\pi}{2}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-\pi=2x-\dfrac{\pi}{2}+k2\pi\\4x-\pi=\dfrac{\pi}{2}-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{4}+\dfrac{k\pi}{3}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{3}\)
2.
\(\Leftrightarrow1-cos^2x+1-sin^24x=2\)
\(\Leftrightarrow cos^2x+sin^24x=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx=0\\sin4x=0\end{matrix}\right.\)
\(\Leftrightarrow cosx=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)

Dao động này có biên độ \(A=5cm\)
Tần số góc là \(5\pi\left(rad/s\right)\)
Chu kì \(T=\dfrac{2\pi}{\omega}=0,4s\)
Và tần số là: \(f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz\)
⇒ Chọn B
