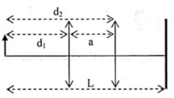
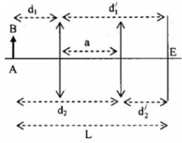
Vật sáng AB đặt song song và cách màn quan sát một khoảng L (hình vẽ). dịch chuyển một thấu kính hội tụ tiêu cự f có trục chính vuông góc với màn ảnh trong khoảng giữa vật và màn ảnh. Khi dịch chuyển tịnh tiến thấu kính dọc trục chính của nó, thì tìm được các vị trí cho ảnh rõ nét trên màn. Phát biểu nào sau đây là sai?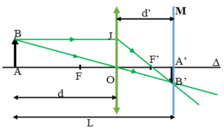
A. Nếu L ≤ 4f thì có thể tìm được một vị trí cho ảnh rõ nét trên màn hình
B. Nếu L > 4f thì có thể tìm được hai vị trí cho ảnh rõ nét trên màn hình
C. Nếu L = 4f thì có thể tìm được một vị trí cho ảnh rõ nét trên màn hình
D. Nếu L ≤ 5f thì có thể tìm được hai vị trí cho ảnh rõ nét trên màn hình.



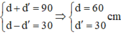
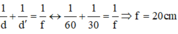
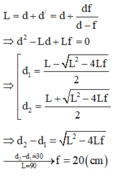
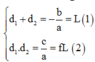


Đáp án: A
Ảnh rõ nét trên màn nên ta có: L = d + d’
Theo công thức thấu kính:
Để có ảnh rõ nét trên màn thì (*) có nghiệm:
∆ ≥ 0 ↔ L ≥ 4 f .