Gọi G là trọng tâm của tam giác ABC với các điểm M N P tùy ý , chứng minh rằng : vectơ GM -NG +GP=AM-NB+CP
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{MB}+4\overrightarrow{MC}\)
\(=6\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{IB}+4\overrightarrow{IC}\)
\(=6\overrightarrow{MI}+4\overrightarrow{IG}+4\overrightarrow{IC}\)
\(=6\overrightarrow{MI}\)
\(\Rightarrow M,I,N\) thẳng hàng

Tham khảo:
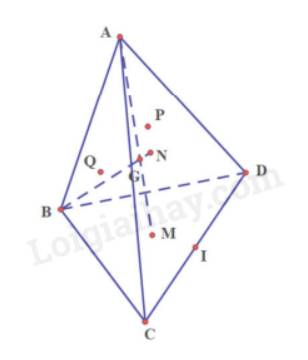
a) Ta có: M là trọng tâm của tam giác BCD
Nên M nằm trên trung tuyến BI (1)
Ta có: N là trọng tâm của tam giác ACD
Nên N nằm trên trung tuyến AI (2)
Từ (1) và (2) suy ra M và N thuộc mp (ABI)
b) Gọi H, K lần lượt là trung điểm của AG, BG
Ta có: HK // AB
AB // MN
Suy ra MN // HK
Theo định lý Ta-let, ta có: \(\frac{{GM}}{{GH}} = \frac{{GN}}{{GK}} = \frac{{MN}}{{HK}}(1)\)
Ta có:\(\frac{{HK}}{{AB}} = \frac{1}{2},\frac{{MN}}{{AB}} = \frac{1}{3}\)
Do đó \(\frac{{MN}}{{AB}}:\frac{{HK}}{{AB}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{HK}} = \frac{2}{3}(2)\)
Từ (1) và (2) suy ra\(\frac{{GM}}{{GH}} = \frac{2}{3}GH = \frac{1}{2}GA \Rightarrow \frac{{GM}}{{\frac{1}{2}GA}} = \frac{2}{3} \Rightarrow \frac{{GM}}{{GA}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GN}}{{GB}} = \frac{1}{3}\)
c) Gọi H, K lần lượt là trung điểm của BC, BD
Tam giác AHD có:\(\frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Suy ra: QM // AD
Do đó, tam giác QGM đồng dạng với tam giác DGA
Nên D, G, Q thẳng hàng
Ta có: QM // AD nên \(\frac{{QM}}{{AD}} = \frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Mà \(\frac{{QM}}{{AD}} = \frac{{QG}}{{GD}}\)
Do đó:\(\frac{{QG}}{{GD}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GP}}{{GC}} = \frac{1}{3}\)
Suy ra điều cần chứng minh.

Do M là trung điểm BC nên: \(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
Tương tự: \(\overrightarrow{BN}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{BC}\) ; \(\overrightarrow{CP}=\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CB}\)
Cộng vế:
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BA}\right)+\dfrac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CA}\right)+\dfrac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CB}\right)=\overrightarrow{0}\)
b. Từ câu a ta có:
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AO}+\overrightarrow{OM}+\overrightarrow{BO}+\overrightarrow{ON}+\overrightarrow{CO}+\overrightarrow{OP}=\overrightarrow{0}\)
\(\Leftrightarrow-\overrightarrow{OA}+\overrightarrow{OM}-\overrightarrow{OB}+\overrightarrow{ON}-\overrightarrow{OC}+\overrightarrow{OP}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OP}\) (đpcm)
Do G là trọng tâm tam giác \(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
Ta có:
\(\overrightarrow{GM}-\overrightarrow{NG}+\overrightarrow{GP}=\left(\overrightarrow{GA}+\overrightarrow{AM}\right)-\left(\overrightarrow{NB}+\overrightarrow{BG}\right)+\left(\overrightarrow{GC}+\overrightarrow{CP}\right)\)
\(=\overrightarrow{GA}-\overrightarrow{BG}+\overrightarrow{GC}+\overrightarrow{AM}-\overrightarrow{BG}+\overrightarrow{CP}\)
\(=\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{AM}-\overrightarrow{BG}+\overrightarrow{CP}\)
\(=\overrightarrow{AM}-\overrightarrow{BG}+\overrightarrow{CP}\)